Lesson 14

Adding and Subtracting with Scientific Notation

Let’s add and subtract using scientific notation to answer questions about animals and the solar system.

Problem 1

Evaluate each expression, giving the answer in scientific notation:

  1.  \(5.3 \times 10^4 + 4.7 \times 10^4\)
  2. \(3.7 \times 10^6 - 3.3 \times 10^6\)
  3. \(4.8 \times 10^{\text-3} + 6.3 \times 10^{\text-3}\)
  4. \(6.6 \times 10^{\text-5} - 6.1 \times 10^{\text-5}\)

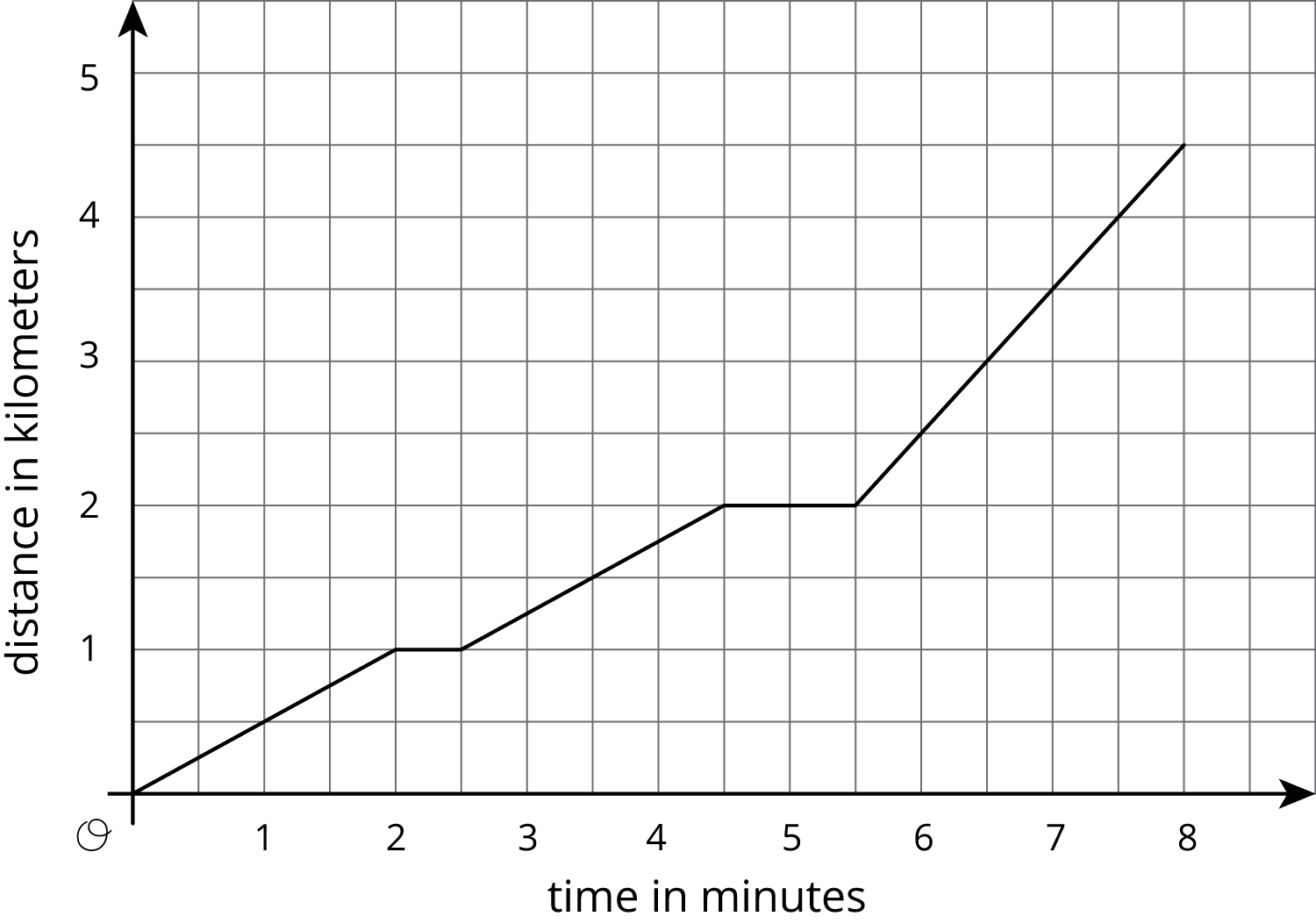
Problem 2

  1. Write a scenario that describes what is happening in the graph.
  2. What is happening at 5 minutes?
  3. What does the slope of the line between 6 and 8 minutes mean?
Coordinate plane, time in minutes, 0 to 8, distance in kilometers, 0 to 5. Line segments connect the origin to 2 comma 1, 2 point 5 comma 1, 4 point 5 comma 2, 5 point 5 comma 2, 8 comma 4 point 5.
(From Unit 6, Lesson 10.)

Problem 3

Apples cost $1 each. Oranges cost $2 each. You have $10 and want to buy 8 pieces of fruit. One graph shows combinations of apples and oranges that total to $10. The other graph shows combinations of apples and oranges that total to 8 pieces of fruit.

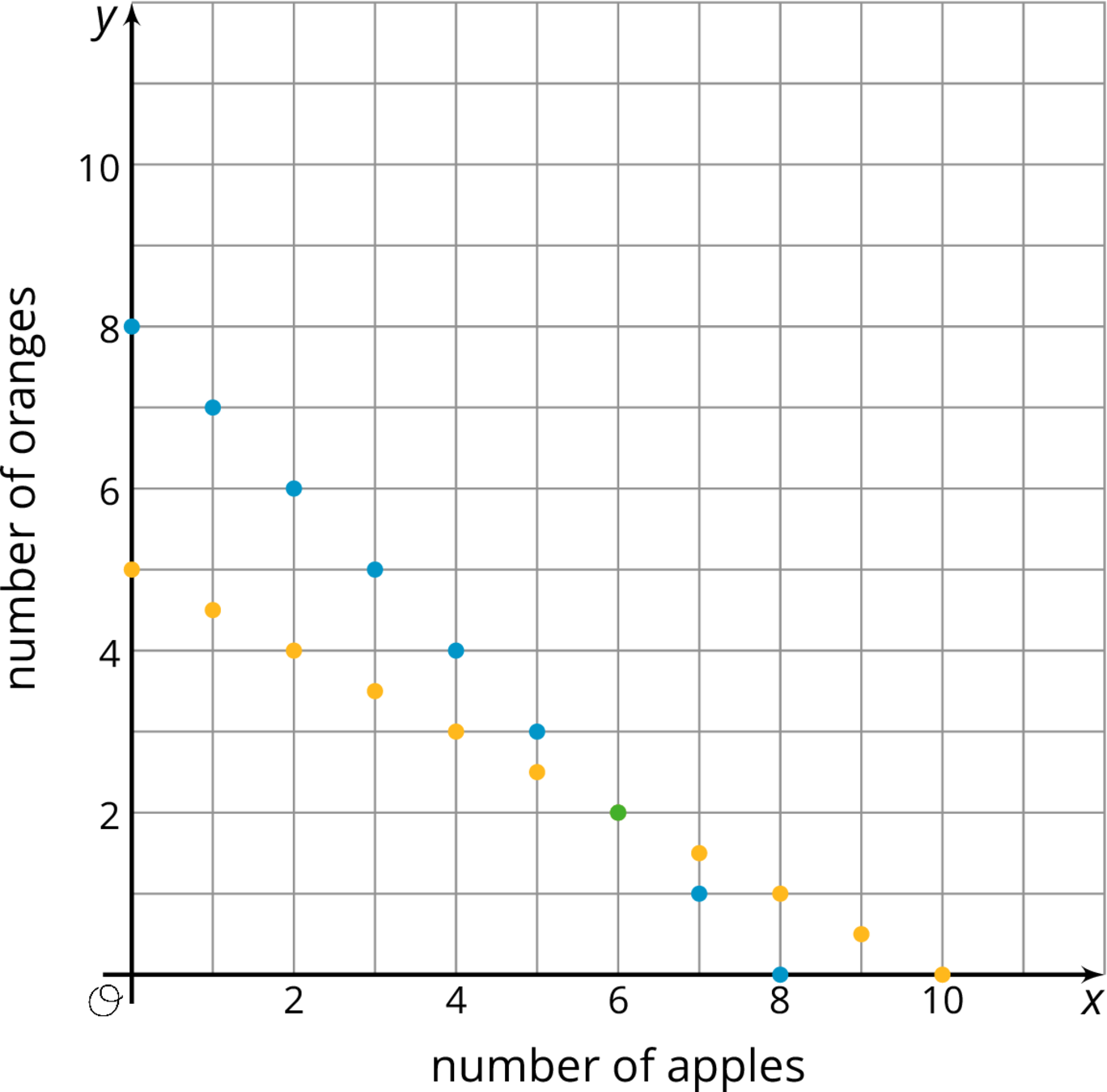
Coordinate plane, x, number of apple, y, number of oranges.

  1. Name one combination of 8 fruits shown on the graph that whose cost does not total to $10.

  2. Name one combination of fruits shown on the graph whose cost totals to $10 that are not 8 fruits all together.

  3. How many apples and oranges would you need to have 8 fruits that cost $10 at the same time?

(From Unit 5, Lesson 12.)

Problem 4

Solve each equation and check your solution.

\(\text-2(3x-4)=4(x+3)+6\)

\(\frac12(z+4)-6=\text-2z+8\)

\(4w-7=6w+31\)

(From Unit 4, Lesson 13.)

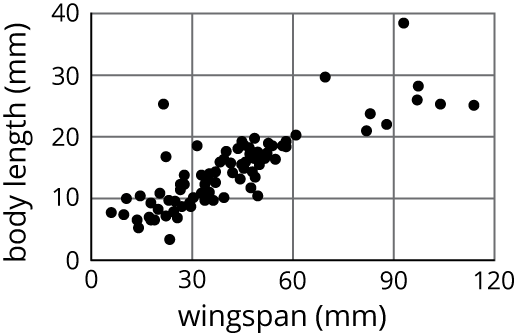
Problem 5

Ecologists measure the body length and wingspan of 127 butterfly specimens caught in a single field.

  1. Draw a line that you think is a good fit for the data.
  2. Write an equation for the line.

     
  3. What does the slope of the line tell you about the wingspans and lengths of these butterflies?
Scatterplot, wingspan in millimeters, body length in millimeters. Please request assistance.
(From Unit 5, Lesson 20.)

Problem 6

The two triangles are similar. Find \(x\).

Two triangles. The first has acute angles marked 46 degrees and x degrees. The second has an obtuse marked 106 degrees.
(From Unit 2, Lesson 12.)