Lesson 15

Decomposing Bases for Area

Let’s look at how some people use volume.

Problem 1

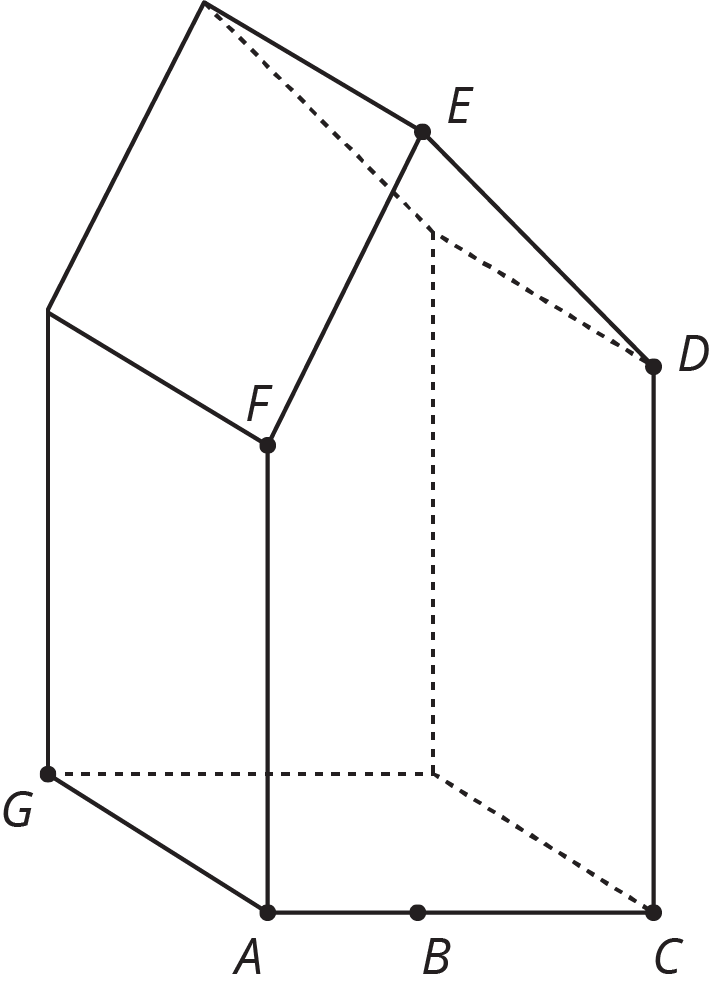
You find a crystal in the shape of a prism. Find the volume of the crystal.

The point \(B\) is directly underneath point \(E\), and the following lengths are known:

  • From \(A\) to \(B\): 2 mm
  • From \(B\) to \(C\): 3 mm
  • From \(A\) to \(F\): 6 mm
  • From \(B\) to \(E\): 10 mm
  • From \(C\) to \(D\): 7 mm
  • From \(A\) to \(G\): 4 mm
An irregular pentagonal prism with base A, F, E, D, C. Segment A, G indicates the height of the prism. Point B lies between A and C.

 

Problem 2

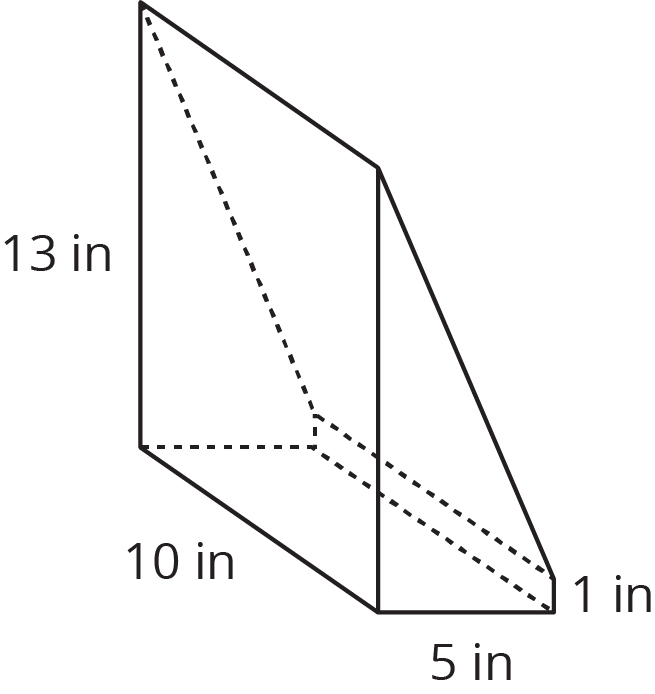
A rectangular prism with dimensions 5 inches by 13 inches by 10 inches was cut to leave a piece as shown in the image. What is the volume of this piece? What is the volume of the other piece not pictured?

A right trapezoidal prism.  Each base is a trapezoid with bases 13 inches and 1 inch, height 5 inches. The prism has height 10 inches.

Problem 3

A triangle has one side that is 7 cm long and another side that is 3 cm long.

  1. Sketch this triangle and label your sketch with the given measures. (If you are stuck, try using a compass or cutting some straws to these two lengths.)

  2. Draw one more triangle with these measures that is not identical to your first triangle.

  3. Explain how you can tell they are not identical.
(From Unit 1, Lesson 17.)

Problem 4

Select all equations that represent a relationship between angles in the figure.

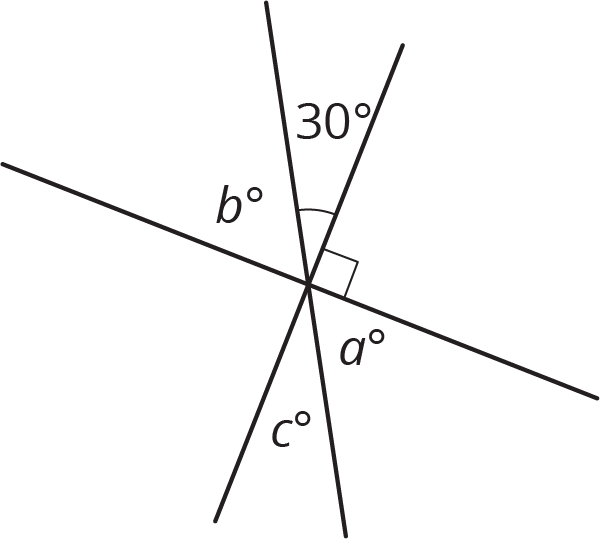
Three points intersect to form 6 lines. Clockwise, the angles measure b degrees, 30 degrees, 90 degrees, a, degrees, c degrees, blank.
A:

\(90-30=b\)

B:

\(30+b=a+c\)

C:

\(a+c+30+b=180\)

D:

\(a=30\)

E:

\(a=c=30\)

F:

\(90+a+c=180\)

(From Unit 1, Lesson 12.)