Lesson 26

Building Prisms

Let’s build a triangular prism from scratch.

26.1: Nets

Here are some nets for various prisms.

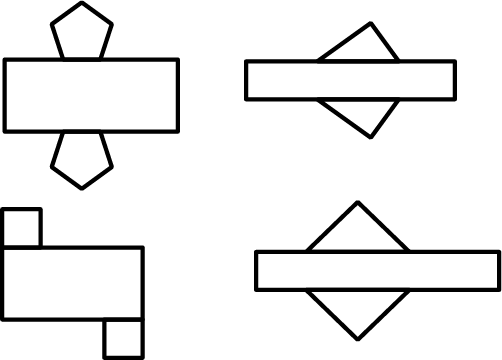
Nets for various prisms. First has a pentagonal base, one has a square base, two have triangular bases. Ask for additional assistance.

  1. What would each net look like when folded?

  2. What do you notice about the nets?

26.2: Making the Base

The base of a triangular prism has one side that is 7 cm long, one side that is 5.5 cm long, and one angle that measures \(45^\circ\).

  1. Draw as many different triangles as you can with these given measurements.

  2. Select one of the triangles you have drawn. Measure and calculate to approximate its area. Explain or show your reasoning.

26.3: Making the Prism

Your teacher will give you an incomplete net. Follow these instructions to complete the net and assemble the triangular prism: 

  1. Draw an identical copy of the triangle you selected in the previous activity along the top of the rectangle, with one vertex on point \(A\).  
  2. Draw another copy of your triangle, flipped upside down, along the bottom of the rectangle, with one vertex on point \(C\).
  3. Determine how long the rectangle needs to be to wrap all the way around your triangular bases. Pause here so your teacher can review your work.
  4. Cut out and assemble your net.

After you finish assembling your triangular prism, answer these questions. Explain or show your reasoning.

  1. What is the volume of your prism?

  2. What is the surface area of your prism?

  3. Stand your prism up so it is sitting on its triangular base.

    1. If you were to cut your prism in half horizontally, what shape would the cross section be?
    2. If you were to cut your prism in half vertically, what shape would the cross section be?

26.4: Combining Prisms

  1. Compare your prism with your partner’s prism. What is the same? What is different?
  2. Find a way you can put your prism and your partner’s prism together to make one new, larger prism. Describe your new prism.
  3. Draw the base of your new prism and label the lengths of the sides.

  4. As you answer these questions about your new prism, look for ways you can use your calculations from the previous activity to help you. Explain or show your reasoning.

    1. What is the area of its base?
    2. What is its height?
    3. What is its volume?
    4. What is its surface area?


How many identical copies of your prism would it take you to put together a new larger prism in which every dimension was twice as long?

Summary