Lesson 11

Slicing Solids

Let's see what shapes you get when you slice a three-dimensional object.

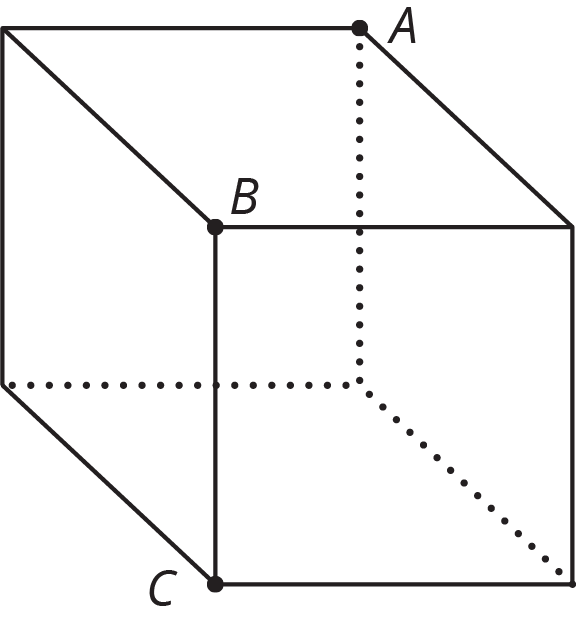
Problem 1

A cube is cut into two pieces by a single slice that passes through points \(A\), \(B\), and \(C\). What shape is the cross section?

A cube is indicated. Point A is located on the back, top right vertex, Point B is located on the front, top left vertex, and Point C is located on the front, bottom left vertex

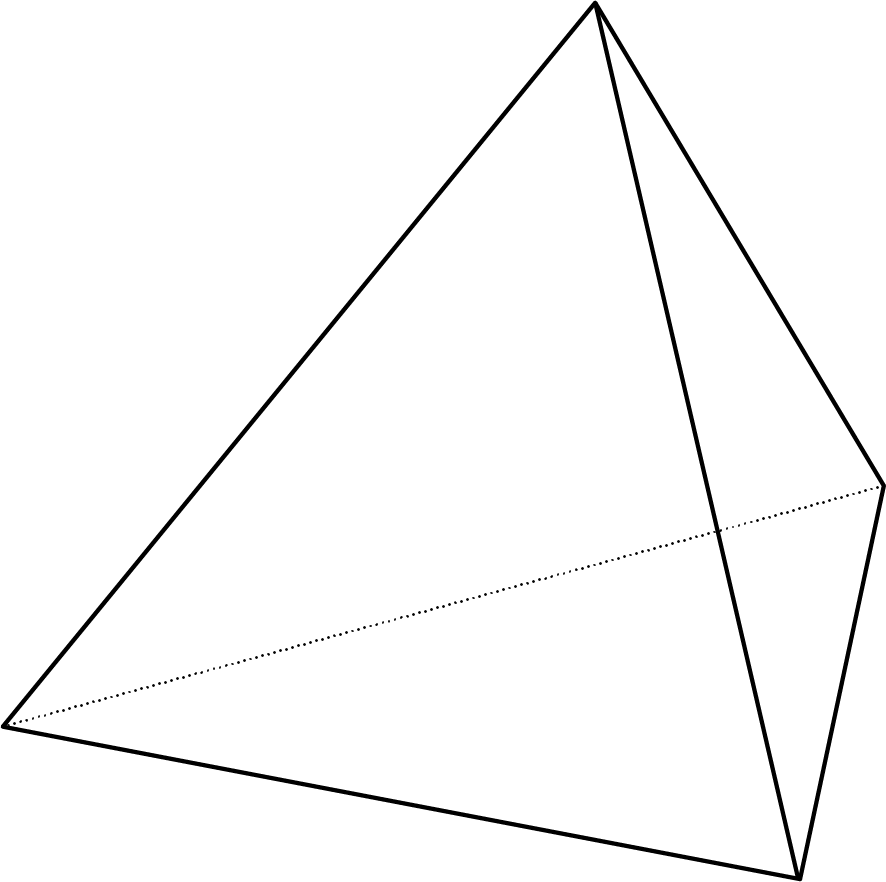
Problem 2

Describe how to slice the three-dimensional figure to result in each cross section.

Three-dimensional figure:

Cross sections:

A pyramid, the base of which is a triangle.
Two figures, a triangle and a trapezoid.

 

Problem 3

Here are two three-dimensional figures.

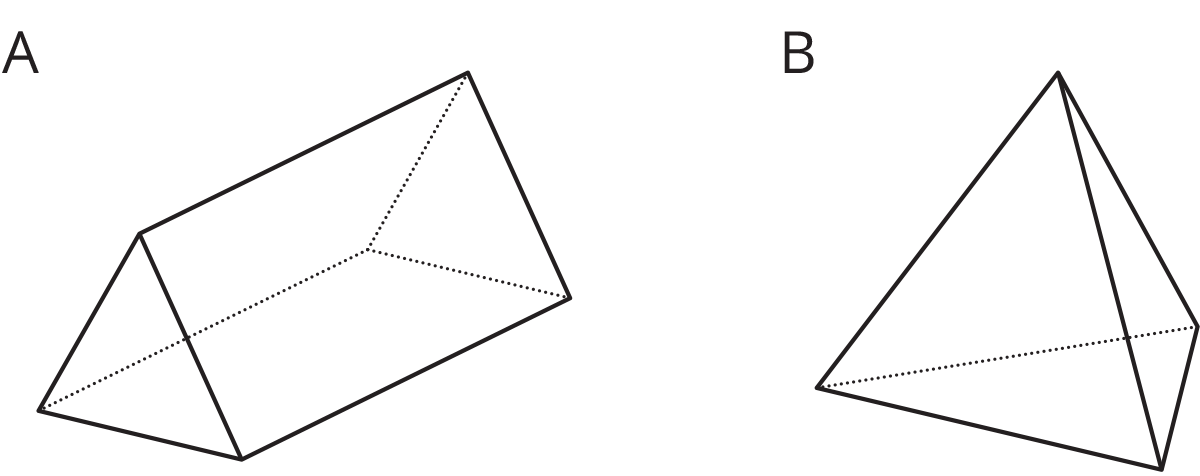
Two three-dimensional figures. Figure A a triangular prism. Figure B is a triangular pyramid.

Describe a way to slice one of the figures so that the cross section is a rectangle.

Problem 4

Each row contains the degree measures of two supplementary angles. Complete the table.

measure of an angle measure of its supplement
\(80^\circ\)
\(25^\circ\)
\(119^\circ\)
\(x\)
(From Unit 1, Lesson 12.)