Lesson 10

Piecewise Linear Functions

Let’s explore functions built out of linear pieces.

Problem 1

The graph shows the distance of a car from home as a function of time.

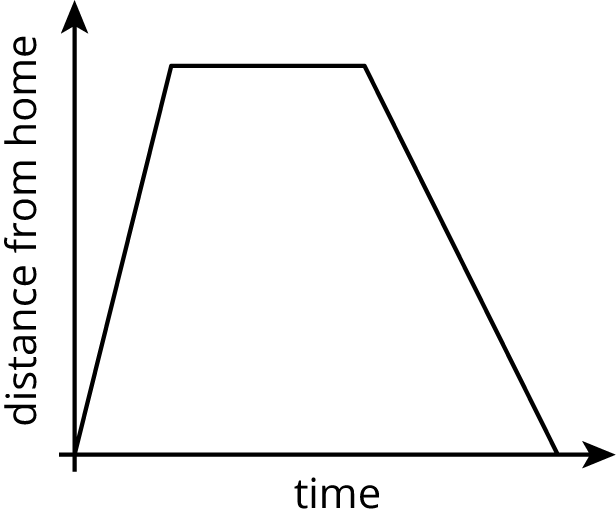
Piecewise graph, horizontal, time, vertical, distance from home. Graph begins at the origin with a positive slope, then a horizontal segment, then a negative slope back to the horizontal axis.

Describe what a person watching the car may be seeing.

Problem 2

The equation and the graph represent two functions. Use the equation \(y=4\) and the graph to answer the questions.

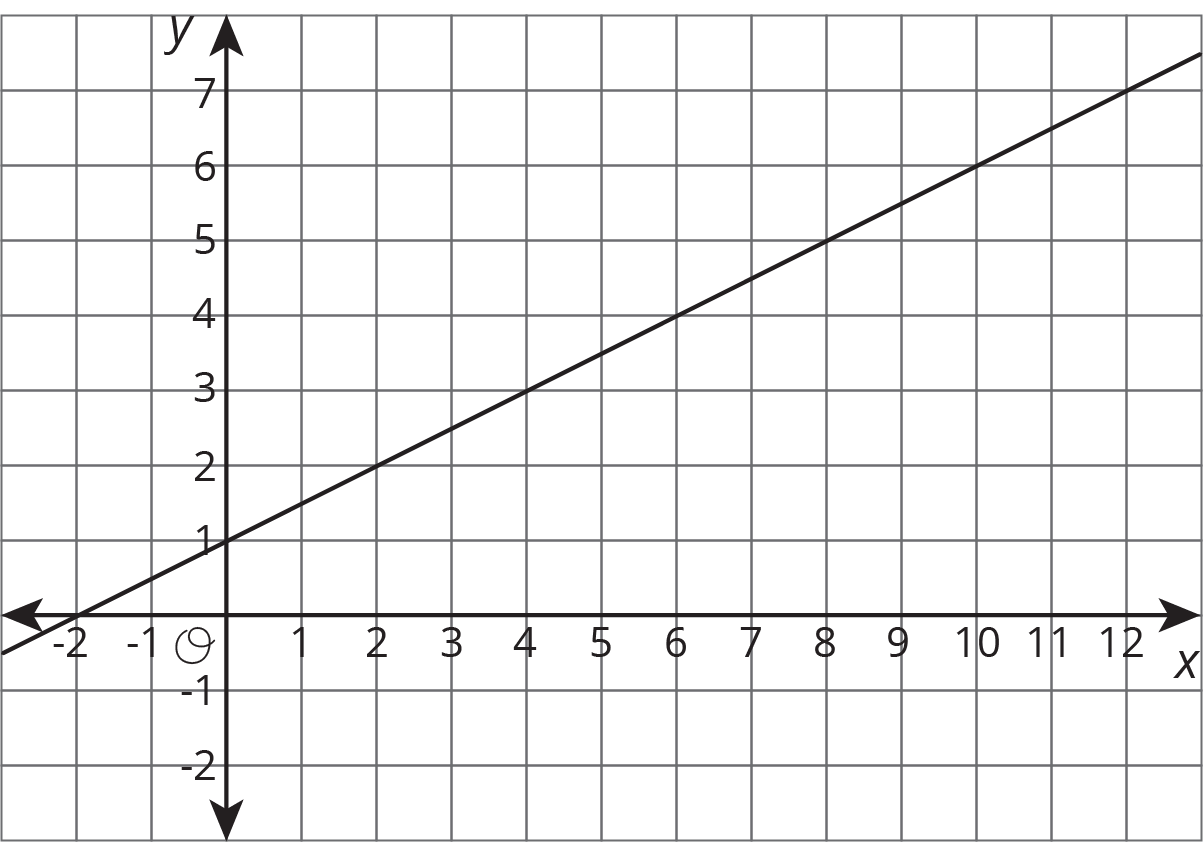
A coordinate plane, x, negative 2 to 12 by ones, y, negative 2 to 7 by ones. A staright line through (negative 2 comma 0), (0 comma 1), (8 comma 5).
  1. When \(x\) is 4, is the output of the equation or the graph greater?
  2. What value for \(x\) produces the same output in both the graph and the equation?
(From Unit 6, Lesson 7.)

Problem 3

This graph shows a trip on a bike trail. The trail has markers every 0.5 km showing the distance from the beginning of the trail.

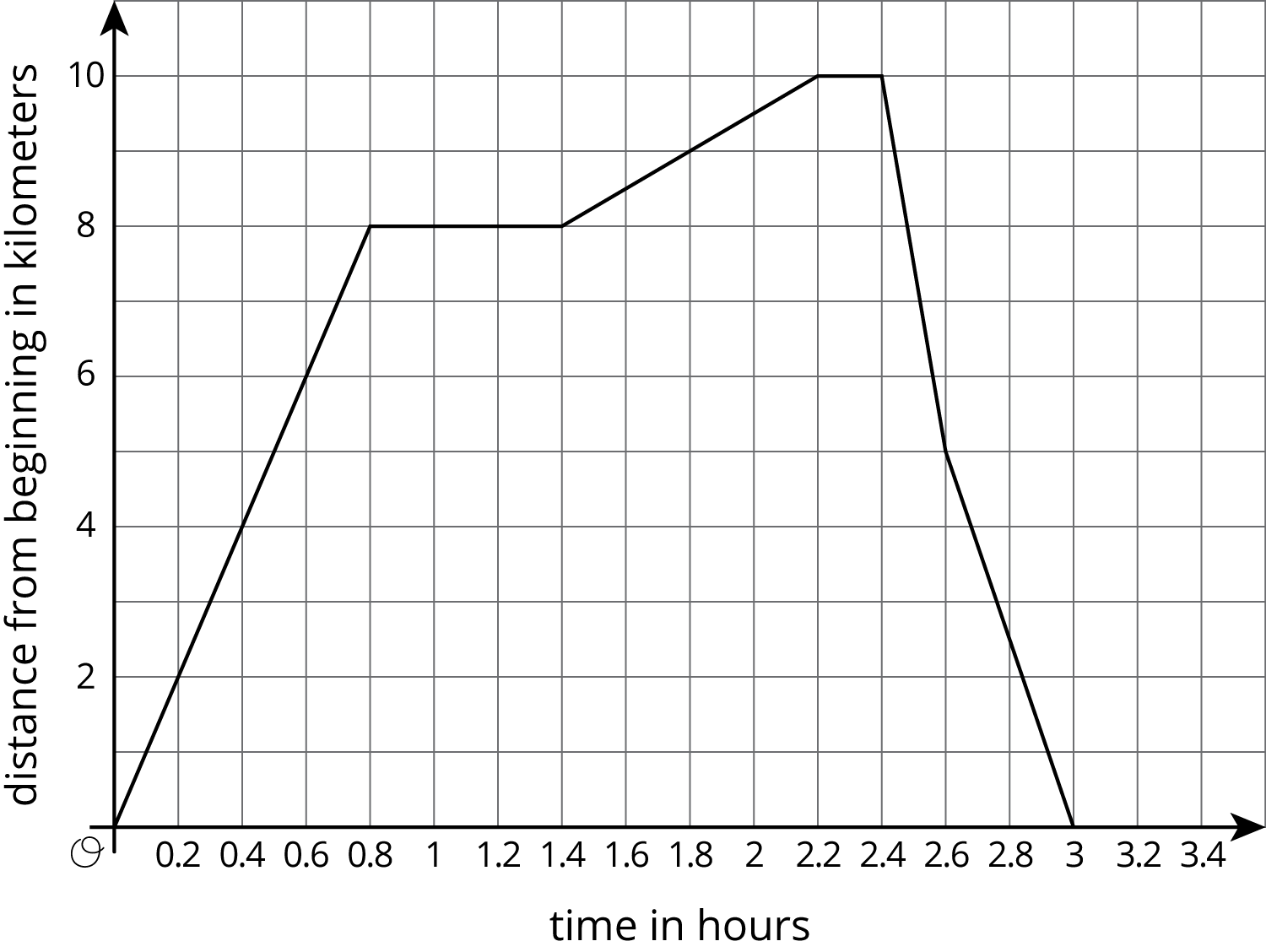
Coordinate plane, x, time in hours, 0 to 3 point 4 by point 2, y, distance from beginning in kilometers, 0 to 10 by 2.

  1. When was the bike rider going the fastest?

  2. When was the bike rider going the slowest?

  3. During what times was the rider going away from the beginning of the trail?

  4. During what times was the rider going back towards the beginning of the trail?

  5. During what times did the rider stop?

Problem 4

The expression \(\text-25t+1250\) represents the volume of liquid of a container after \(t\) seconds. The expression \(50t+250\) represents the volume of liquid of another container after \(t\) seconds. What does the equation \(\text-25t+1250=50t+250\) mean in this situation?

(From Unit 4, Lesson 17.)