Lesson 9

Dealing with Negative Numbers

Let’s show that doing the same to each side works for negative numbers too.

Problem 1

Solve each equation.

  1. \(4x=\text-28\)
  2. \(x-\text-6=\text-2\)
  3. \(\text-x+4=\text-9\)
  4. \(\text-3x+7=1\)
  5. \(25x+\text-11=\text-86\)

Problem 2

Here is an equation \(2x+9=\text-15\). Write three different equations that have the same solution as \(2x+9=\text-15\). Show or explain how you found them.

Problem 3

Select all the equations that match the diagram.

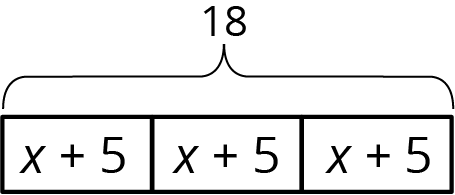
Tape diagram, 3 equal parts each marked x + 5, total 18.
A:

\(x+5=18\)

B:

\(18\div3=x+5\)

C:

\(3(x+5)=18\)

D:

\(x+5 = \frac13\boldcdot 18\)

E:

\(3x+5=18\)

(From Unit 3, Lesson 3.)

Problem 4

There are 88 seats in a theater. The seating in the theater is split into 4 identical sections. Each section has 14 red seats and some blue seats.

  1. Draw a tape diagram to represent the situation.
  2. What unknown amounts can be found by by using the diagram or reasoning about the situation?
(From Unit 3, Lesson 2.)

Problem 5

Match each story to an equation.

A:

A stack of nested paper cups is 8 inches tall. The first cup is 4 inches tall and each of the rest of the cups in the stack adds \(\frac14\) inch to the height of the stack.

B:

A baker uses 4 cups of flour. She uses \(\frac14\) cup to flour the counters and the rest to make 8 identical muffins.

C:

Elena has an 8-foot piece of ribbon. She cuts off a piece that is \(\frac14\) of a foot long and cuts the remainder into four pieces of equal length.

1:

\(\frac14 + 4x=8\)

2:

\(4+\frac14x=8\)

3:

\(8x +\frac14=4\)

(From Unit 3, Lesson 4.)