Lesson 7
Reasoning about Solving Equations (Part 1)
Let’s see how a balanced hanger is like an equation and how moving its weights is like solving the equation.
7.1: Hanger Diagrams
In the two diagrams, all the triangles weigh the same and all the squares weigh the same.
For each diagram, come up with . . .
- One thing that must be true
- One thing that could be true
- One thing that cannot possibly be true

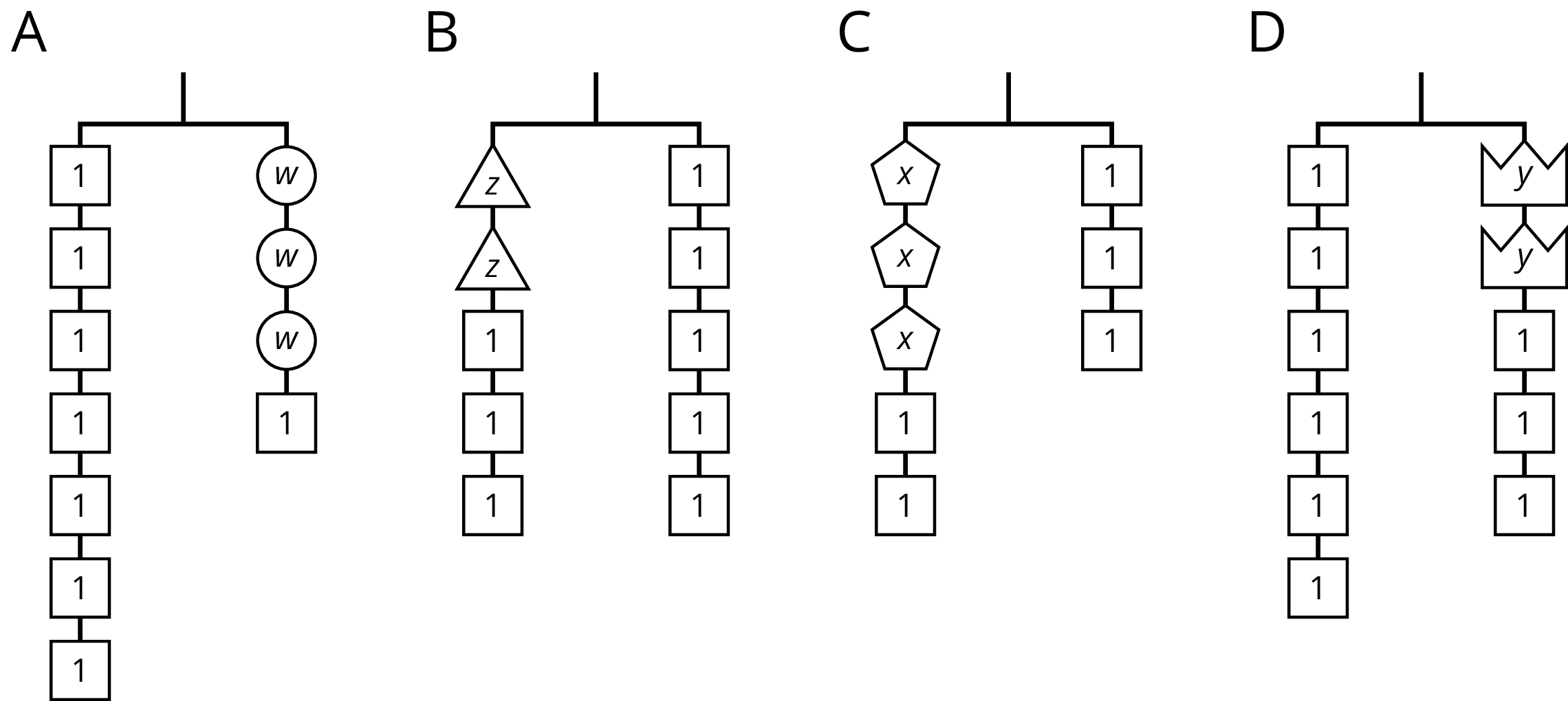
7.2: Hanger and Equation Matching
On each balanced hanger, figures with the same letter have the same weight.
- Match each hanger to an equation. Complete the equation by writing \(x\), \(y\), \(z\), or \(w\) in the empty box.
- \(2 \boxed{\phantom{3}} + 3 = 5\)
- \(3 \boxed{\phantom{3}} + 2 = 3\)
- \(6 = 2 \boxed{\phantom{3}} + 3\)
-
\(7 = 3 \boxed{\phantom{3}} + 1\)
- Find the solution to each equation. Use the hanger to explain what the solution means.
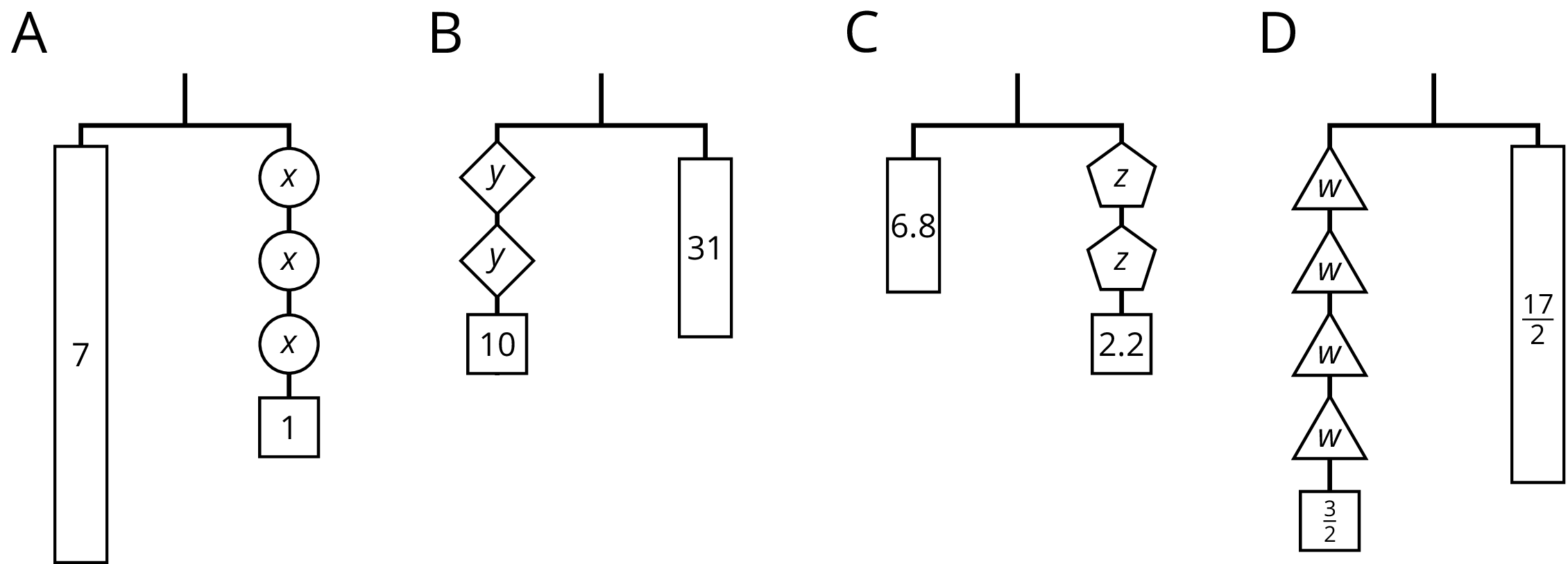
7.3: Use Hangers to Understand Equation Solving
Here are some balanced hangers where each piece is labeled with its weight. For each diagram:
- Write an equation.
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the diagram.
- Explain how to figure out the weight of a piece labeled with a letter by reasoning about the equation.
Summary
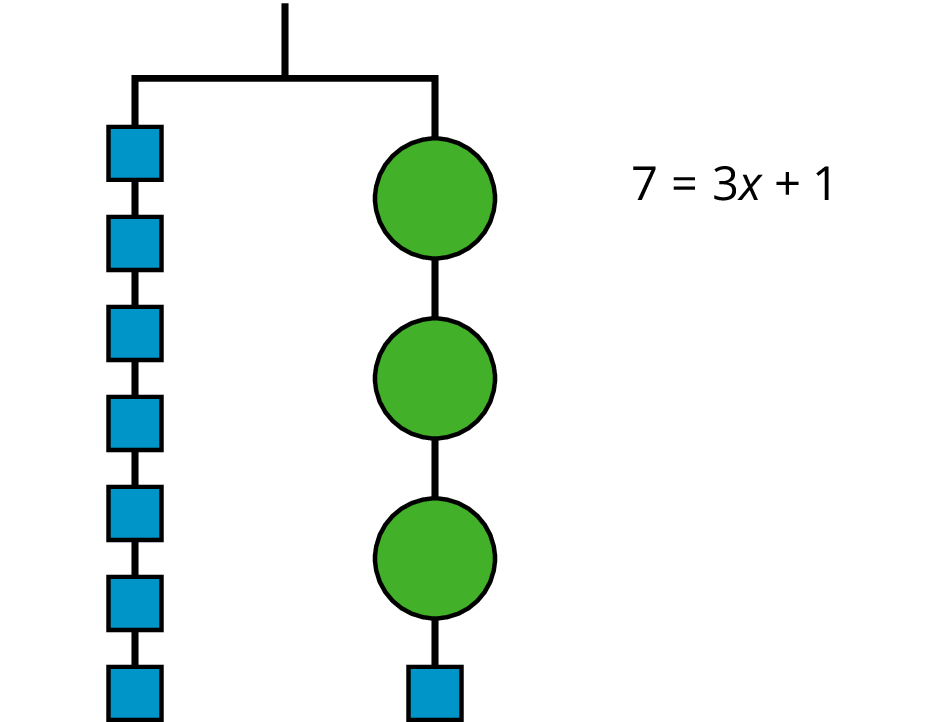
In this lesson, we worked with two ways to show that two amounts are equal: a balanced hanger and an equation. We can use a balanced hanger to think about steps to finding an unknown amount in an associated equation.
The hanger shows a total weight of 7 units on one side that is balanced with 3 equal, unknown weights and a 1-unit weight on the other. An equation that represents the relationship is \(7=3x+1\).
We can remove a weight of 1 unit from each side and the hanger will stay balanced. This is the same as subtracting 1 from each side of the equation.
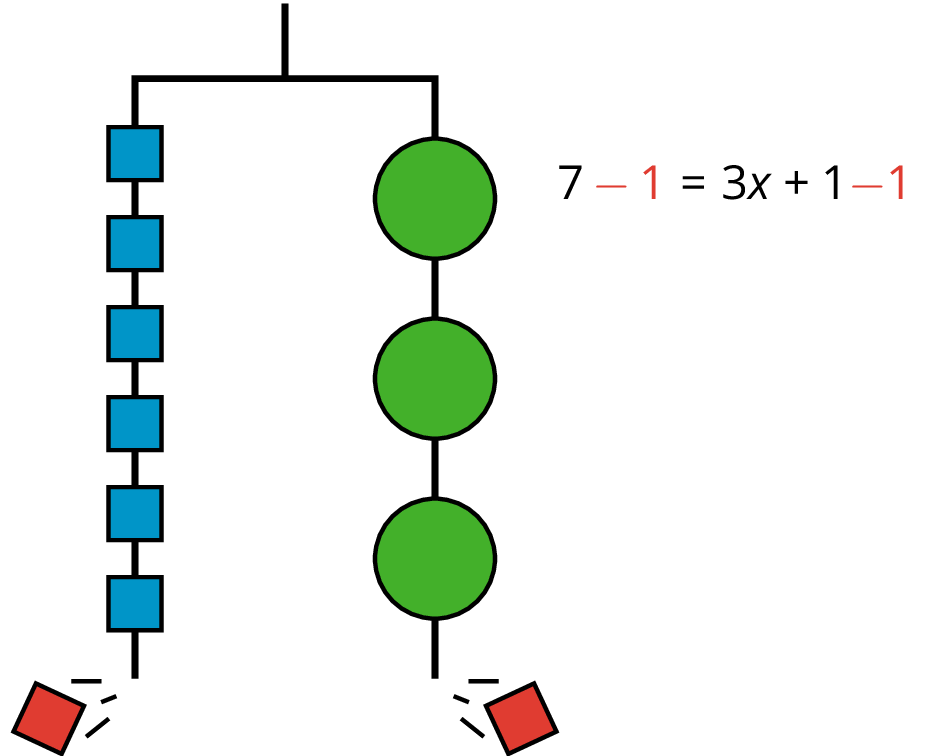
An equation for the new balanced hanger is \(6=3x\).
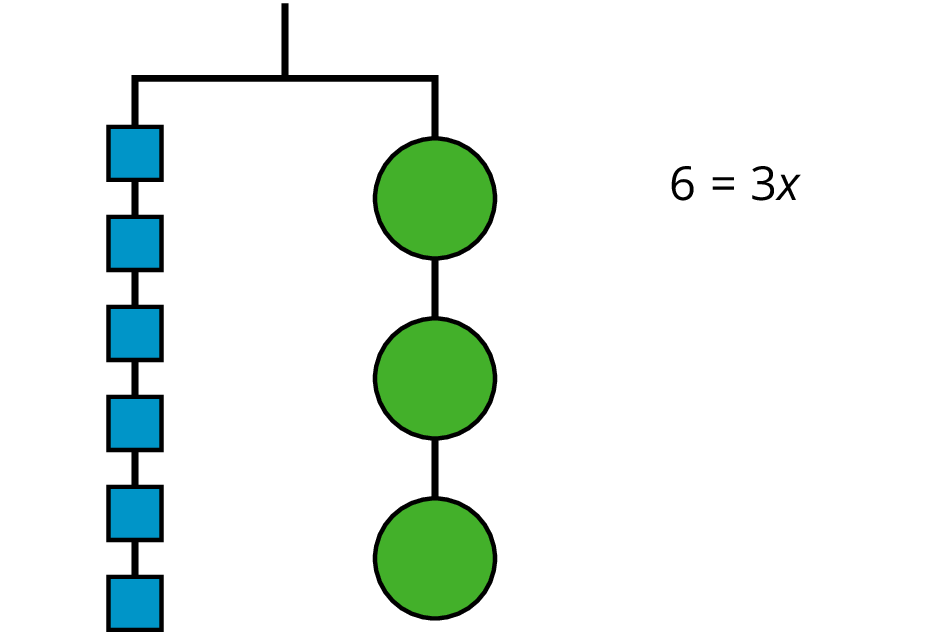
So the hanger will balance with \(\frac13\) of the weight on each side: \(\frac13 \boldcdot 6 = \frac13 \boldcdot 3x\).
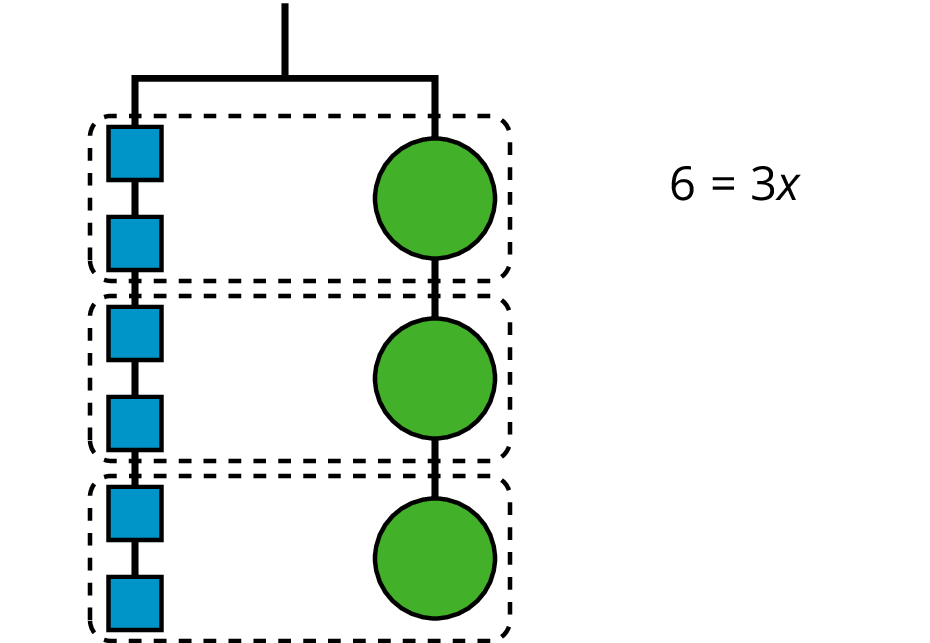
The two sides of the hanger balance with these weights: 6 1-unit weights on one side and 3 weights of unknown size on the other side.
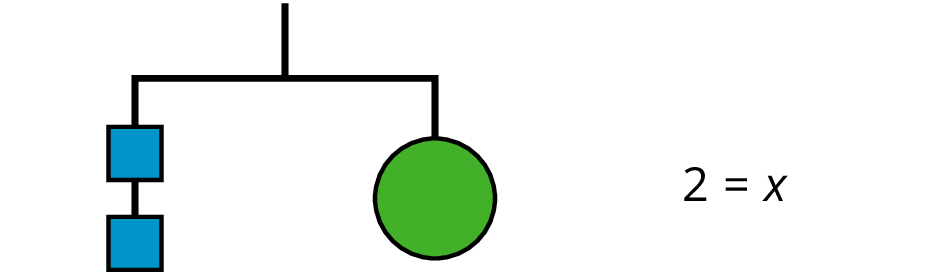
Here is a concise way to write the steps above:
\(\begin {align} 7&=3x+1 & \\ 6&=3x & \text{after subtracting 1 from each side} \\ 2 &= x & \text{after multiplying each side by } \tfrac13 \\ \end{align}\)