Lesson 4
Reasoning about Equations and Tape Diagrams (Part 1)
Let’s see how tape diagrams can help us answer questions about unknown amounts in stories.
Problem 1
Here are three stories:
-
A family buys 6 tickets to a show. They also pay a \$3 parking fee. They spend \$27 to see the show.
-
Diego has 27 ounces of juice. He pours equal amounts for each of his 3 friends and has 6 ounces left for himself.
-
Jada works for 6 hours preparing for the art fair. She spends 3 hours on a sculpture and then paints 27 picture frames.
Here are three equations:
- \(3x+6=27\)
- \(6x+3=27\)
- \(27x+3=6\)
- Decide which equation represents each story. What does \(x\) represent in each equation?
- Find the solution to each equation. Explain or show your reasoning.
- What does each solution tell you about its situation?
Problem 2
Here is a diagram and its corresponding equation. Find the solution to the equation and explain your reasoning.
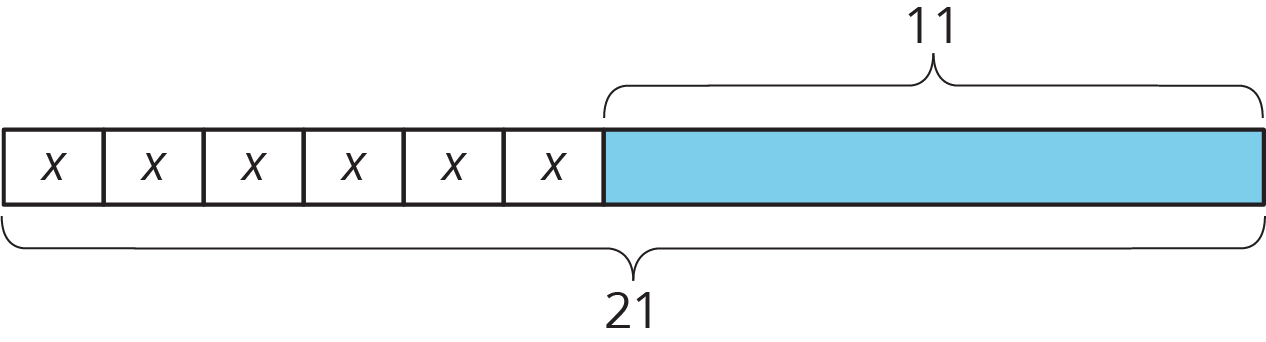
\(6x+11=21\)
Problem 3
For each object, choose an appropriate scale for a drawing that fits on a regular sheet of paper. Not all of the scales on the list will be used.
Objects
- A person
- A football field (120 yards by 53\(\frac{1}{3}\) yards)
- The state of Washington (about 240 miles by 360 miles)
- The floor plan of a house
- A rectangular farm (6 miles by 2 mile)
Scales
- 1 in : 1 ft
- 1 cm : 1 m
- 1: 1000
- 1 ft: 1 mile
- 1: 100,000
- 1 mm: 1 km
- 1: 10,000,000
Problem 4
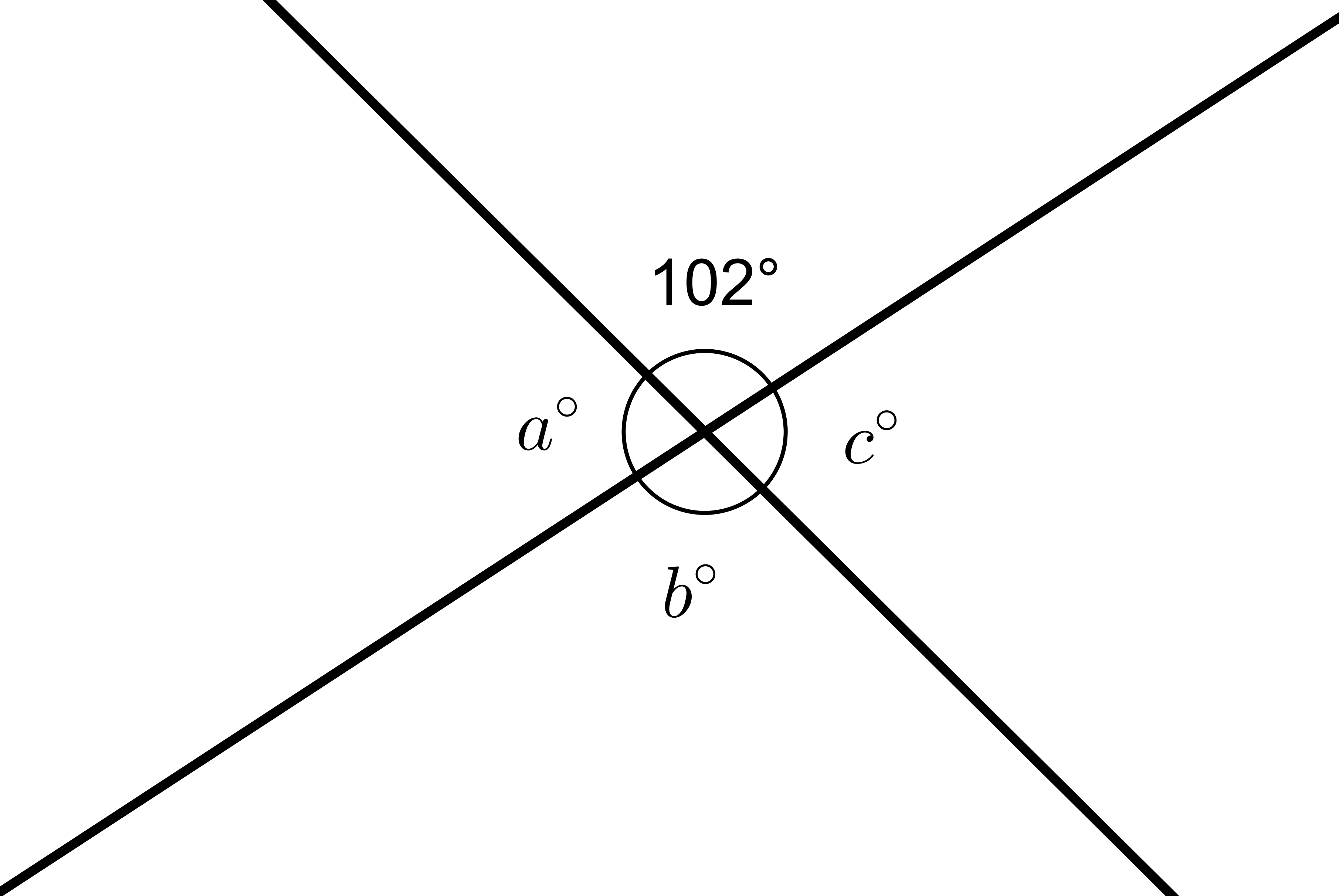
The diagram shows two intersecting lines.
Find the missing angle measures.