Lesson 13
Using Equations to Solve for Unknown Angles
Let’s figure out missing angles using equations.
Problem 1
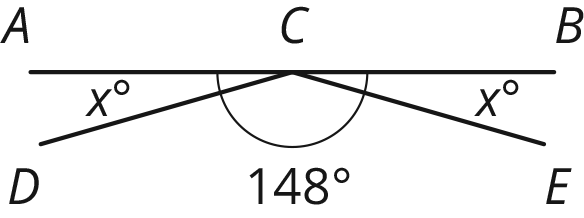
Segments \(AB\), \(DC\), and \(EC\) intersect at point \(C\). Angle \(DCE\) measures \(148^\circ\). Find the value of \(x\).
Problem 2
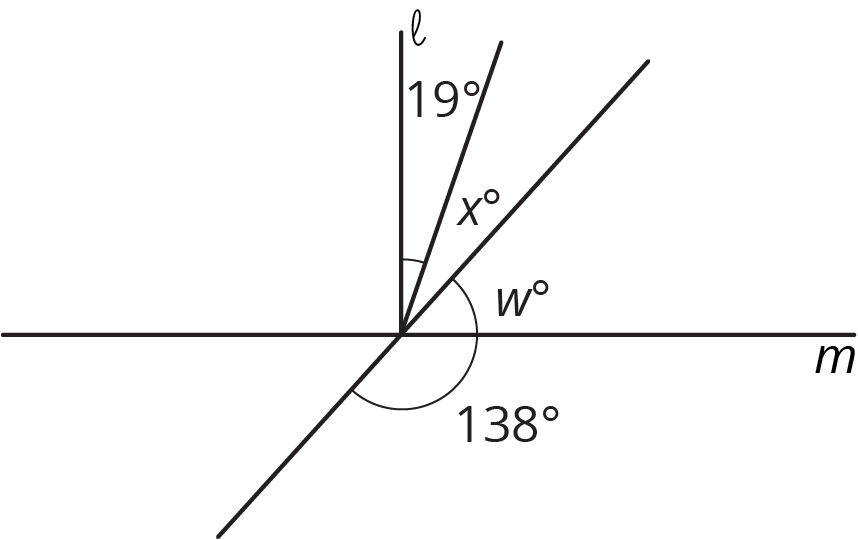
Line \(\ell\) is perpendicular to line \(m\). Find the value of \(x\) and \(w\).
Problem 3
If you knew that two angles were complementary and were given the measure of one of those angles, would you be able to find the measure of the other angle? Explain your reasoning.
Problem 4
Here is a polygon on a grid.

-
Draw a scaled copy of the polygon using a scale factor 3. Label the copy A.
-
Draw a scaled copy of the polygon with a scale factor \(\frac{1}{2}\). Label it B.
-
Is Polygon A a scaled copy of Polygon B? If so, what is the scale factor that takes B to A?
Problem 5
Jada, Elena, and Lin walked a total of 37 miles last week. Jada walked 4 more miles than Elena, and Lin walked 2 more miles than Jada. The diagram represents this situation:
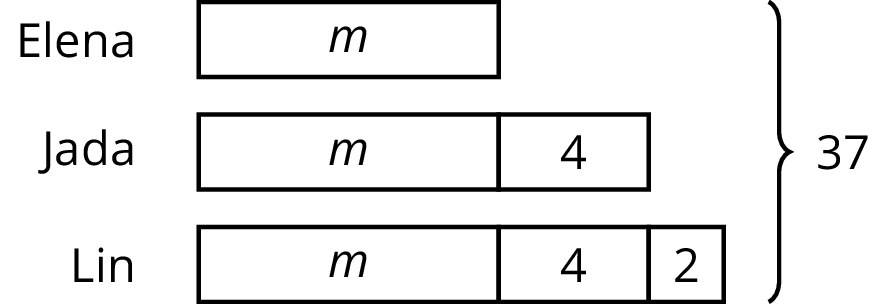
Find the number of miles that they each walked. Explain or show your reasoning.