Lesson 3

Rectangle Madness

Let’s cut up rectangles.

3.1: Squares in Rectangles

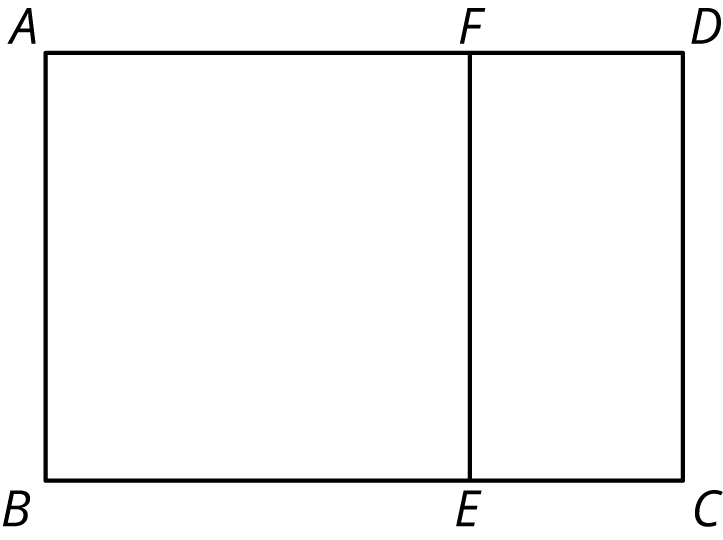
  1. Rectangle \(ABCD\) is not a square. Rectangle \(ABEF\) is a square.

    A rectangle is labeled ABCD with horizontal side BC below horizontal side AD. Vertical line segment FE is drawn creating square ABEF.

    1. Suppose segment \(AF\) were 5 units long and segment \(FD\) were 2 units long. How long would segment \(AD\) be?

    2. Suppose segment \(BC\) were 10 units long and segment \(BE\) were 6 units long. How long would segment \(EC\) be?

    3. Suppose segment \(AF\) were 12 units long and segment \(FD\) were 5 units long. How long would segment \(FE\) be?

    4. Suppose segment \(AD\) were 9 units long and segment \(AB\) were 5 units long. How long would segment \(FD\) be?

  2. Rectangle \(JKXW\) has been decomposed into squares.

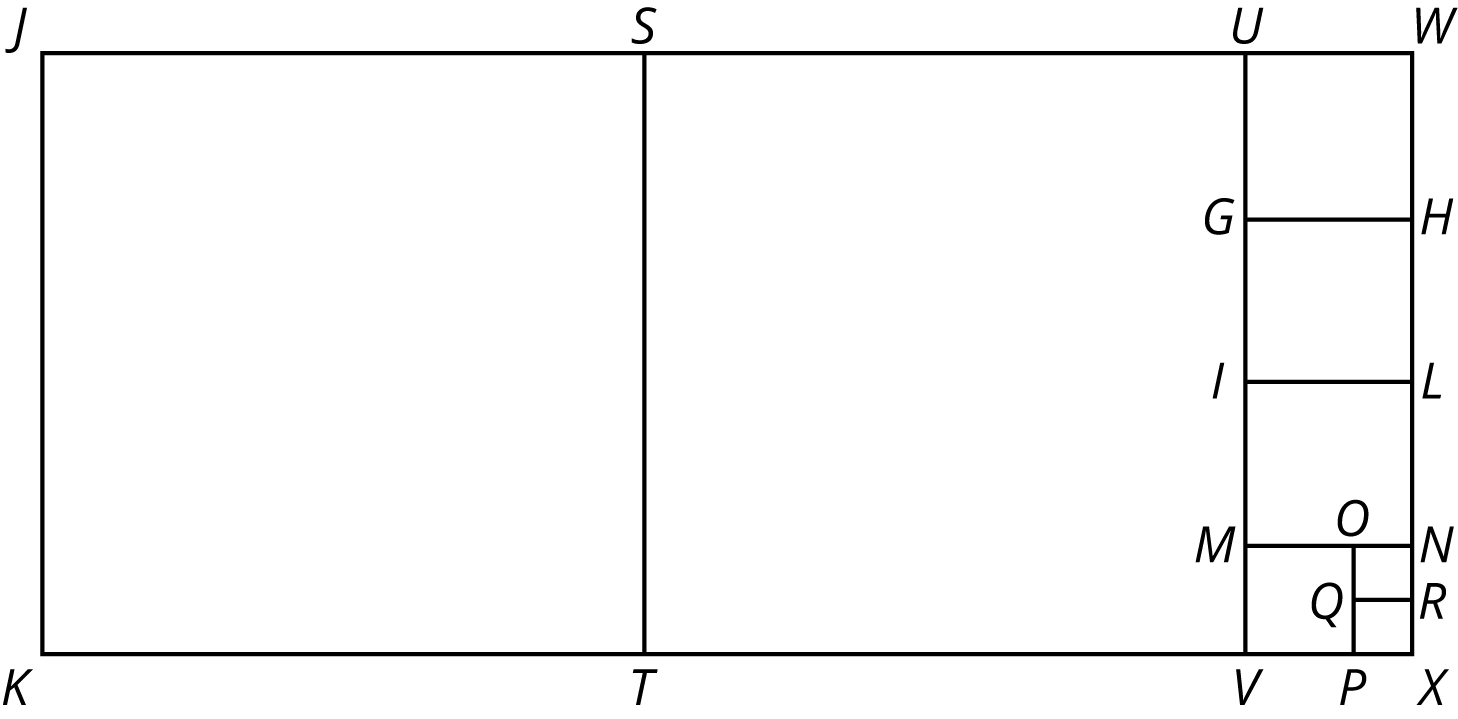
    Tiling of rectangle KXWJ with 2 large squares, 3 medium squares, 1 small square, and 2 tiny squares.

    Segment \(JK\) is 33 units long and segment \(JW\) is 75 units long. Find the areas of all of the squares in the diagram.

  3. Rectangle \(ABCD\) is 16 units by 5 units.

    A rectangle labeled ABCD is indicated with horizontal side AB below horizontal side DC.

      

    1. In the diagram, draw a line segment that decomposes \(ABCD\) into two regions: a square that is the largest possible and a new rectangle.

    2. Draw another line segment that decomposes the new rectangle into two regions: a square that is the largest possible and another new rectangle.

    3. Keep going until rectangle \(ABCD\) is entirely decomposed into squares.

    4. List the side lengths of all the squares in your diagram.


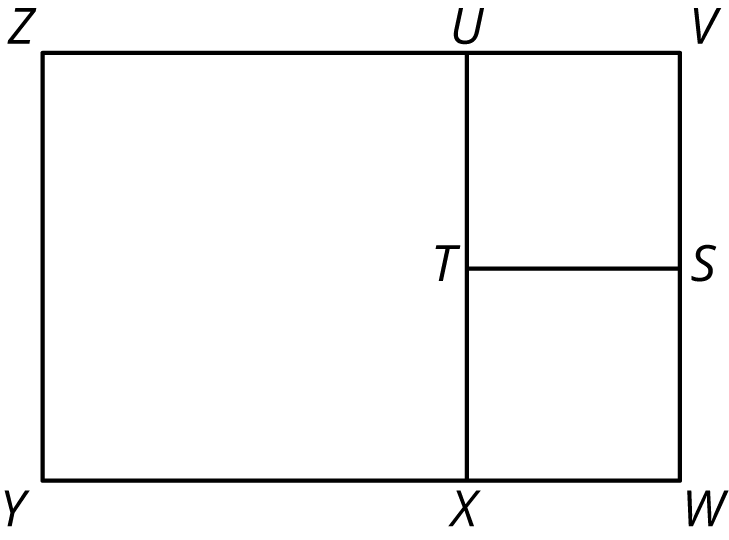
Rectangle VWYZ is decomposed into 3 squares. 

  1. The diagram shows that rectangle \(VWYZ\) has been decomposed into three squares. What could the side lengths of this rectangle be?

  2. How many different side lengths can you find for rectangle \(VWYZ\)?

  3. What are some rules for possible side lengths of rectangle \(VWYZ\)?

3.2: More Rectangles, More Squares

  1. Draw a rectangle that is 21 units by 6 units.

     

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until the diagram shows that your original rectangle has been entirely decomposed into squares.

    2. How many squares of each size are in your diagram?

    3. What is the side length of the smallest square?

  2. Draw a rectangle that is 28 units by 12 units.

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until the diagram shows that your original rectangle has been decomposed into squares.

    2. How many squares of each size are in your diagram?

    3. What is the side length of the smallest square?

  3. Write each of these fractions as a mixed number with the smallest possible numerator and denominator:

    1. \(\frac{16}{5}\)

    2. \(\frac{21}{6}\)

    3. \(\frac{28}{12}\)

  4. What do the fraction problems have to do with the previous rectangle decomposition problems?

3.3: Finding Equivalent Fractions

  1. Accurately draw a rectangle that is 9 units by 4 units.

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until your original rectangle has been entirely decomposed into squares.

    2. How many squares of each size are there?

    3. What are the side lengths of the last square you drew?

    4. Write \(\frac94\) as a mixed number.

  2. Accurately draw a rectangle that is 27 units by 12 units.

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until your original rectangle has been entirely decomposed into squares.

    2. How many squares of each size are there?

    3. What are the side lengths of the last square you drew?

    4. Write \(\frac{27}{12}\) as a mixed number.

    5. Compare the diagram you drew for this problem and the one for the previous problem. How are they the same? How are they different?

  3. What is the greatest common factor of 9 and 4? What is the greatest common factor of 27 and 12? What does this have to do with your diagrams of decomposed rectangles?



We have seen some examples of rectangle tilings. A tiling means a way to completely cover a shape with other shapes, without any gaps or overlaps. For example, here is a tiling of rectangle \(KXWJ\) with 2 large squares, 3 medium squares, 1 small square, and 2 tiny squares.

Tiling of rectangle KXWJ with 2 large squares, 3 medium squares, 1 small square, and 2 tiny squares.

Some of the squares used to tile this rectangle have the same size.

Might it be possible to tile a rectangle with squares where the squares are all different sizes?

If you think it is possible, find such a rectangle and such a tiling. If you think it is not possible, explain why it is not possible.

3.4: It’s All About Fractions

  1. Accurately draw a 37-by-16 rectangle. (Use graph paper, if possible.)

     

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until your original rectangle has been entirely decomposed into squares.

    2. How many squares of each size are there?

    3. What are the dimensions of the last square you drew?

    4. What does this have to do with \(2+\frac{1}{3+\frac15}\)?

  2. Consider a 52-by-15 rectangle.

     

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until your original rectangle has been entirely decomposed into squares.

    2. Write a fraction equal to this expression: \(3+\frac{1}{2+\frac17}\).

    3. Notice some connections between the rectangle and the fraction.

    4. What is the greatest common factor of 52 and 15?

  3. Consider a 98-by-21 rectangle.

     

    1. In your rectangle, draw a line segment that decomposes the rectangle into a new rectangle and a square that is as large as possible. Continue until your original rectangle has been entirely decomposed into squares.

    2. Write a fraction equal to this expression: \(4+\frac{1}{1+\frac{7}{14}}\).

    3. Notice some connections between the rectangle and the fraction.

    4. What is the greatest common factor of 98 and 21?

  4. Consider a 121-by-38 rectangle.

     

    1. Use the decomposition-into-squares process to write a continued fraction for \(\frac{121}{38}\). Verify that it works.

    2. What is the greatest common factor of 121 and 38?

Summary