Lesson 9
Two Graphs for Each Relationship
Let’s use tables, equations, and graphs to answer questions about proportional relationships.
Problem 1
At the supermarket you can fill your own honey bear container. A customer buys 12 oz of honey for $5.40.
- How much does honey cost per ounce?
- How much honey can you buy per dollar?
- Write two different equations that represent this situation. Use \(h\) for ounces of honey and \(c\) for cost in dollars.

- Choose one of your equations, and sketch its graph. Be sure to label the axes.
Problem 2
The point \((3, \frac65)\) lies on the graph representing a proportional relationship. Which of the following points also lie on the same graph? Select all that apply.
\((1, 0.4)\)
\((1.5, \frac{6}{10})\)
\((\frac65, 3)\)
\((4, \frac{11}{5})\)
\((15, 6)\)
Problem 3
A trail mix recipe asks for 4 cups of raisins for every 6 cups of peanuts. There is proportional relationship between the amount of raisins, \(r\) (cups), and the amount of peanuts, \(p\) (cups), in this recipe.
- Write the equation for the relationship that has constant of proportionality greater than 1. Graph the relationship.
- Write the equation for the relationship that has constant of proportionality less than 1. Graph the relationship.
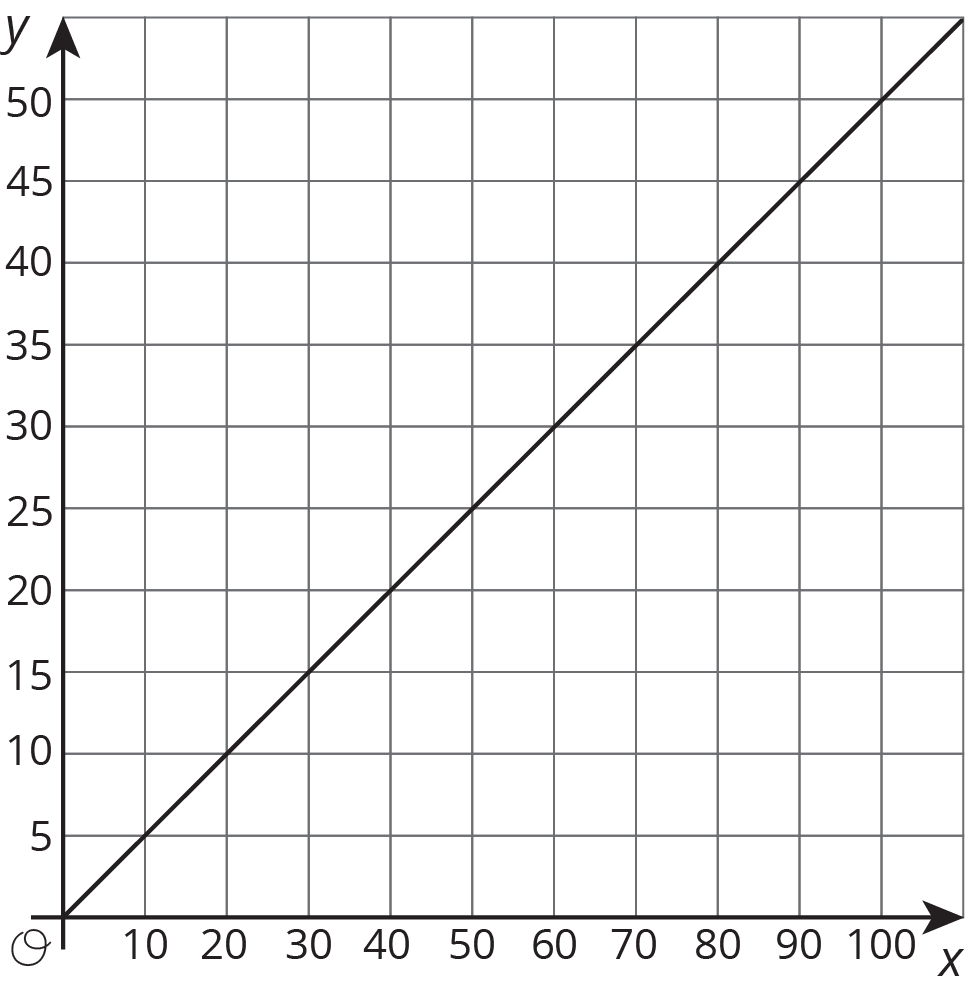
Problem 4
Here is a graph that represents a proportional relationship.
- Come up with a situation that could be represented by this graph.
- Label the axes with the quantities in your situation.
- Give the graph a title.
- Choose a point on the graph. What do the coordinates represent in your situation?