Lesson 7
Graphs of Proportional Relationships
Let's see how graphs of proportional relationships differ from graphs of other relationships.
Problem 1
A lemonade recipe calls for \(\frac14\) cup of lemon juice for every cup of water.
- Use the table to answer these questions.
- What does \(x\) represent?
- What does \(y\) represent?
- Is there a proportional relationship between \(x\) and \(y\)?
- Plot the pairs in the table in a coordinate plane.
| \(x\) | \(y\) |
|---|---|
| 1 | \(\frac14\) |
| 2 | \(\frac12\) |
| 3 | \(\frac34\) |
| 4 | 1 |
Problem 2
There is a proportional relationship between the number of months a person has had a streaming movie subscription and the total amount of money they have paid for the subscription. The cost for 6 months is $47.94. The point \((6, 47.94)\) is shown on the graph below.
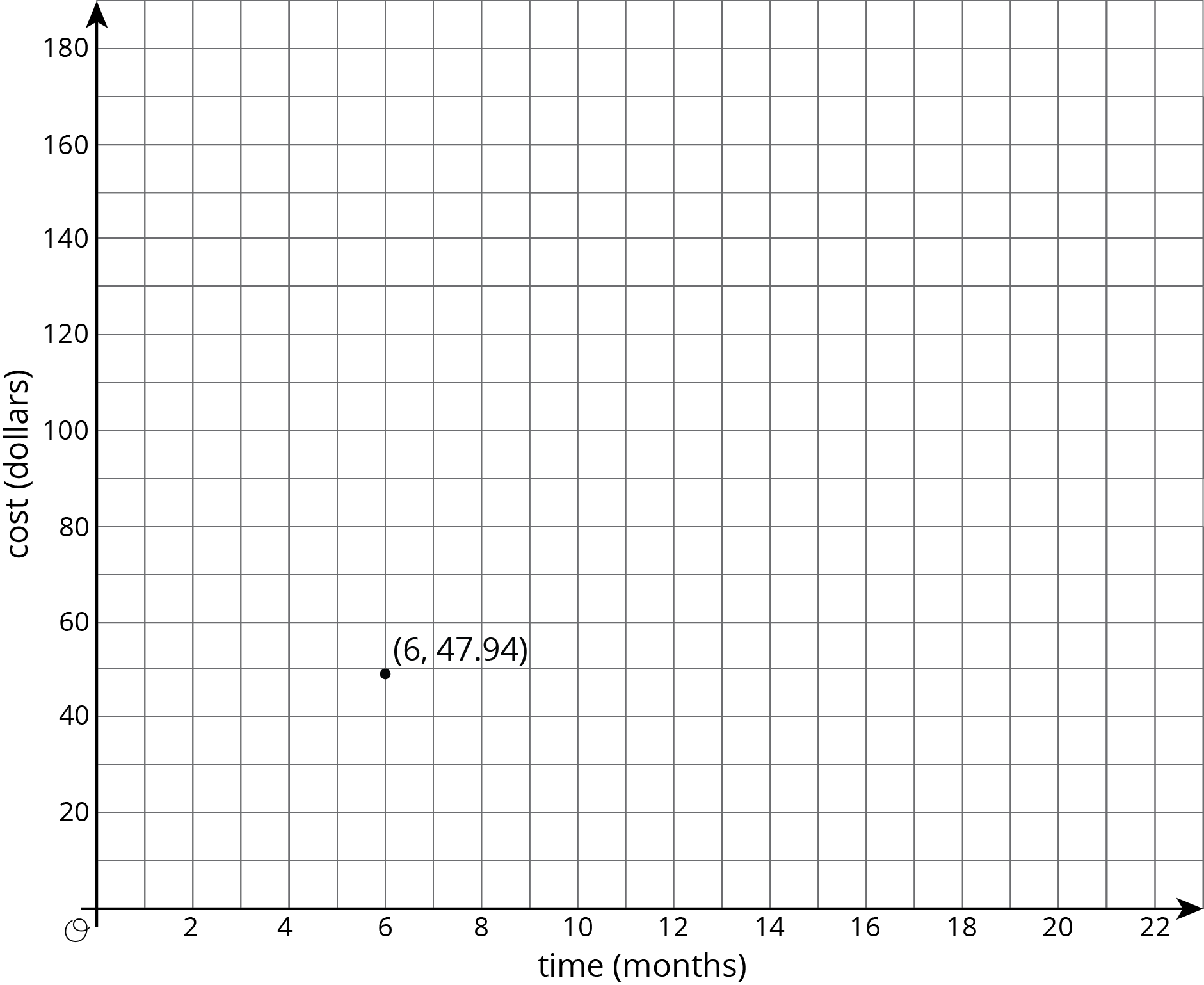
- What is the constant of proportionality in this relationship?
- What does the constant of proportionality tell us about the situation?
- Add at least three more points to the graph and label them with their coordinates.
- Write an equation that represents the relationship between \(C\), the total cost of the subscription, and \(m\), the number of months.
Problem 3
The graph shows the amounts of almonds, in grams, for different amounts of oats, in cups, in a granola mix. Label the point \((1, k)\) on the graph, find the value of \(k\), and explain its meaning.
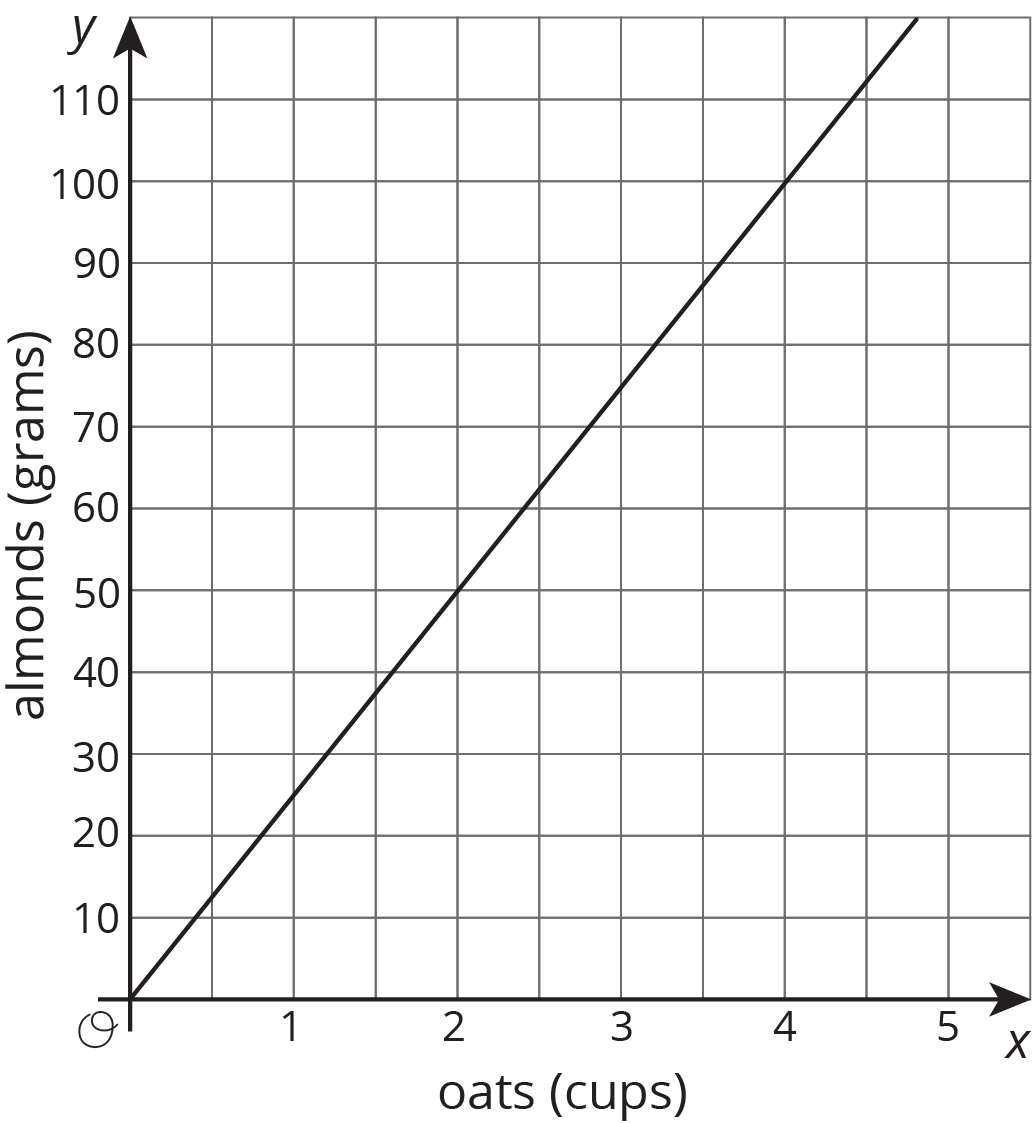
Problem 4
Select all the pieces of information that would tell you \(x\) and \(y\) have a proportional relationship. Let \(y\) represent the distance in meters between a rock and a turtle's current position and \(x\) represent the time in minutes the turtle has been moving.
\(y = 3x\)
After 4 minutes, the turtle has walked 12 feet away from the rock.
The turtle walks for a bit, then stops for a minute before walking again.
The turtle walks away from the rock at a constant rate.
Problem 5
What information do you need to know to write an equation relating two quantities that have a proportional relationship?