Lesson 2

Keeping the Equation Balanced

Let's figure out unknown weights on balanced hangers.

Problem 1

Which of the changes would keep the hanger in balance?

Select all that apply.

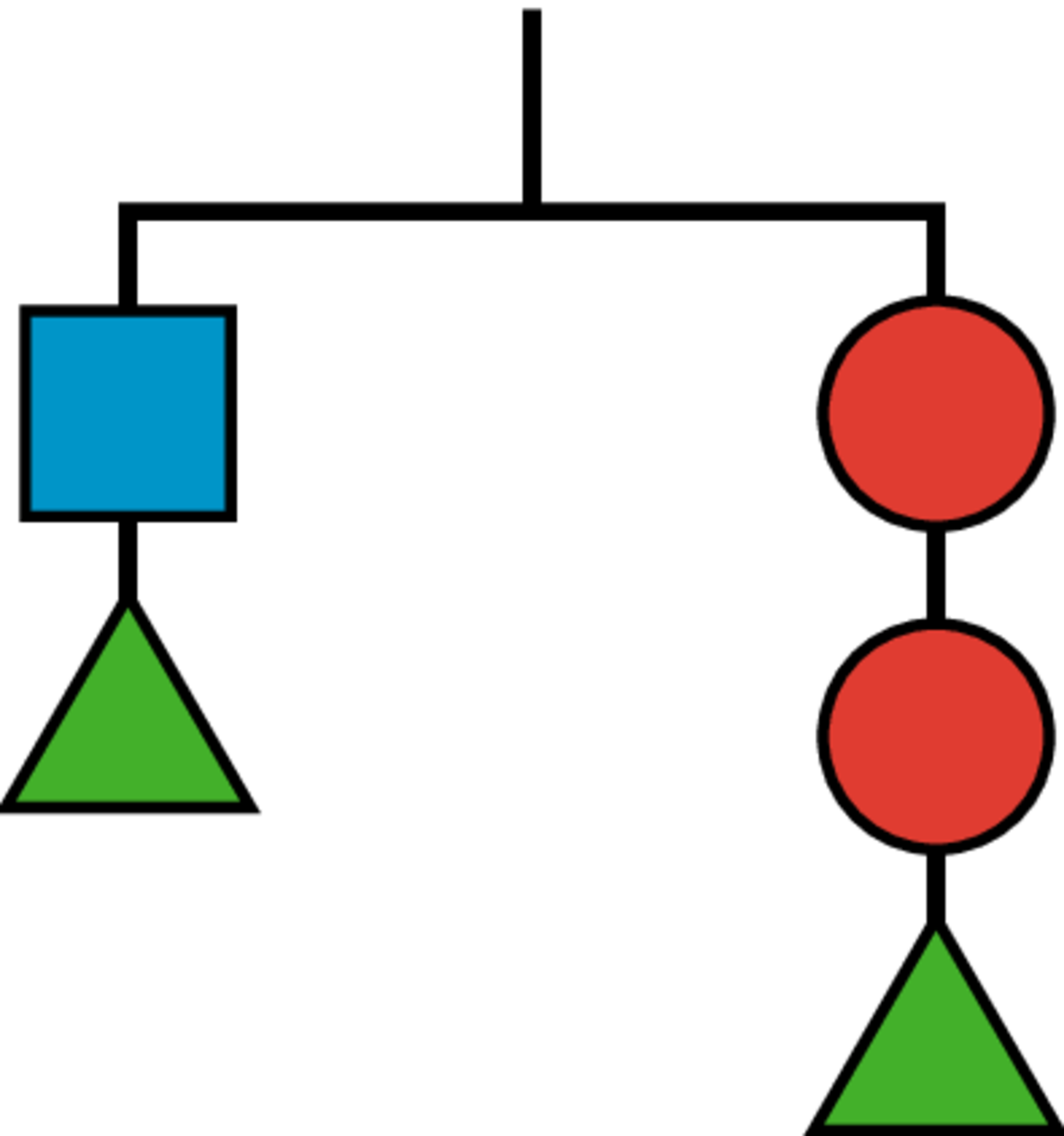
Balanced hanger. Left side, 1 triangle and 1 square. Right side, 2 circles and 1 triangle.

 

A:

Adding two circles on the left and a square on the right

B:

Adding 2 triangles to each side

C:

Adding two circles on the right and a square on the left

D:

Adding a circle on the left and a square on the right

E:

Adding a triangle on the left and a square on the right

Problem 2

Here is a balanced hanger diagram.

Each triangle weighs 2.5 pounds, each circle weighs 3 pounds, and \(x\) represents the weight of each square. Select all equations that represent the hanger.

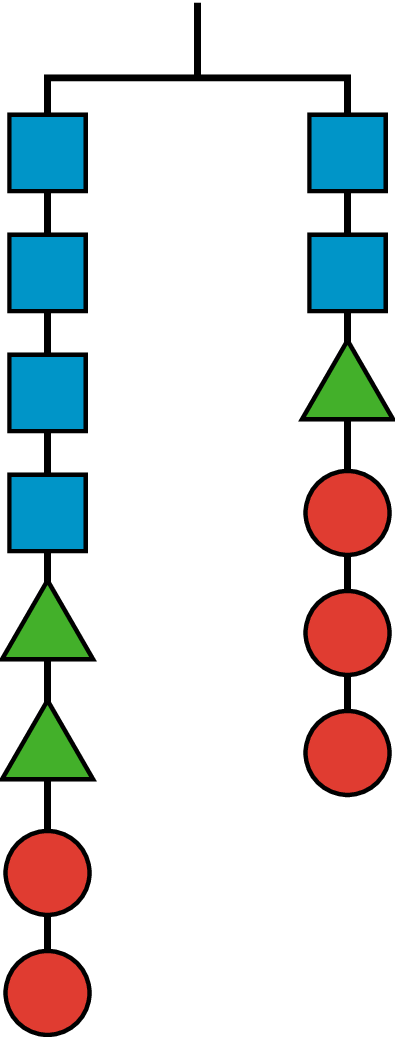
A balanced hanger. Left side, 4 squares, 2 triangles, 2 circles. Right side, 2 squares, 1 triangle, 3 circles.
A:

\(x+x+x+x+11=x+11.5\)

B:

\(2x=0.5\)

C:

\(4x+5+6=2x+2.5+6\)

D:

\(2x+2.5=3\)

E:

\(4x+2.5+2.5+3+3=2x+2.5+3+3+3\)

Problem 3

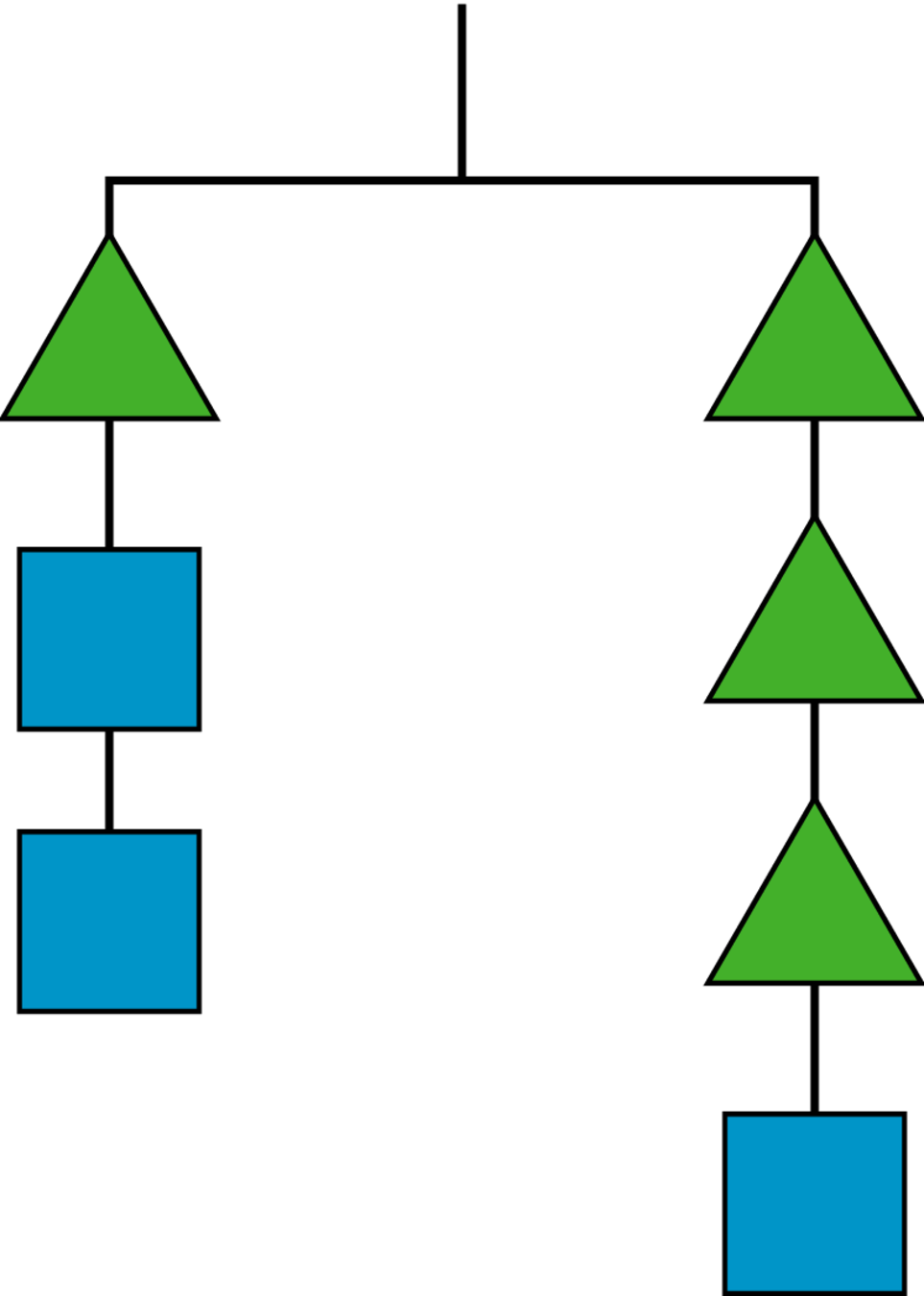
What is the weight of a square if a triangle weighs 4 grams?

Explain your reasoning.

Balanced hanger. Left side, 1 triangle, 2 squares. Right side, 3 triangles, 1 square. 

Problem 4

Andre came up with the following puzzle. “I am three years younger than my brother, and I am 2 years older than my sister. My mom's age is one less than three times my brother's age. When you add all our ages, you get 87. What are our ages?”

  1. Try to solve the puzzle.

  2. Jada writes this equation for the sum of the ages: \((x)+(x+3)+(x-2) + 3(x+3) - 1=87\).

    Explain the meaning of the variable and each term of the equation.

  3. Write the equation with fewer terms.

  4. Solve the puzzle if you haven’t already.

(From Unit 4, Lesson 1.)

Problem 5

These two lines are parallel. Write an equation for each.

Two lines in an x y plane. 
(From Unit 3, Lesson 8.)