Lesson 12
Systems of Equations
Let’s learn what a system of equations is.
Problem 1
Here is the graph for one equation in a system of equations:
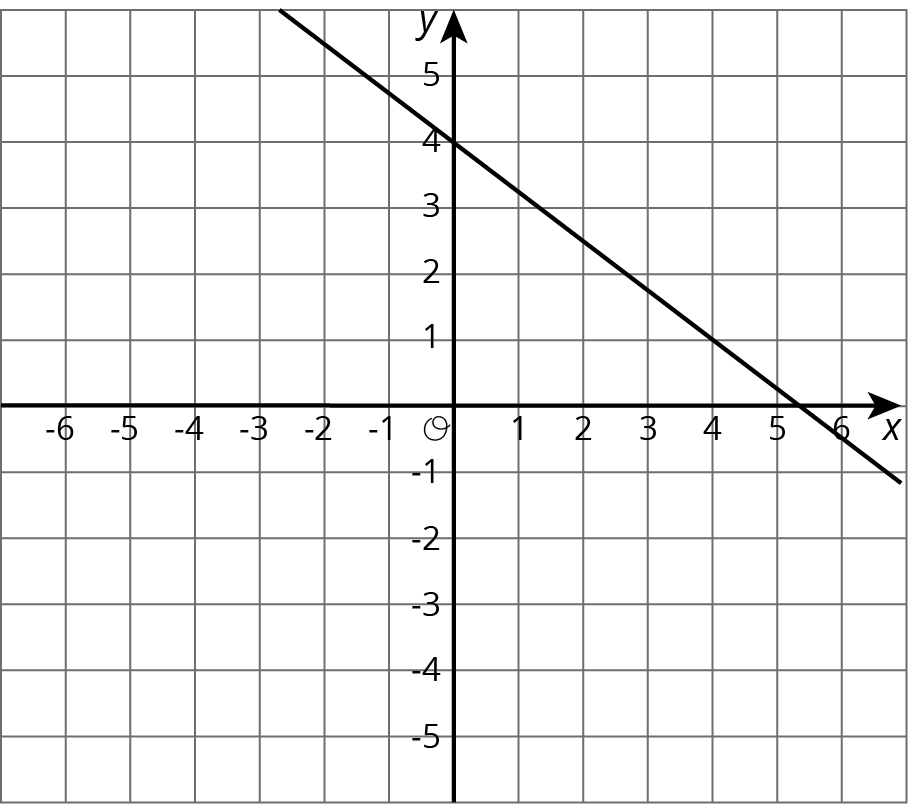
- Write a second equation for the system so it has infinitely many solutions.
- Write a second equation whose graph goes through \((0,1)\) so the system has no solutions.
- Write a second equation whose graph goes through \((0,2)\) so the system has one solution at \((4,1)\).
Problem 2
Create a second equation so the system has no solutions.
\(\begin{cases} y=\frac34x -4 \\ \\ \end{cases}\)
Problem 3
Andre is in charge of cooking broccoli and zucchini for a large group. He has to spend all $17 he has and can carry 10 pounds of veggies. Zucchini costs $1.50 per pound and broccoli costs $2 per pound. One graph shows combinations of zucchini and broccoli that weigh 10 pounds and the other shows combinations of zucchini and broccoli that cost $17.
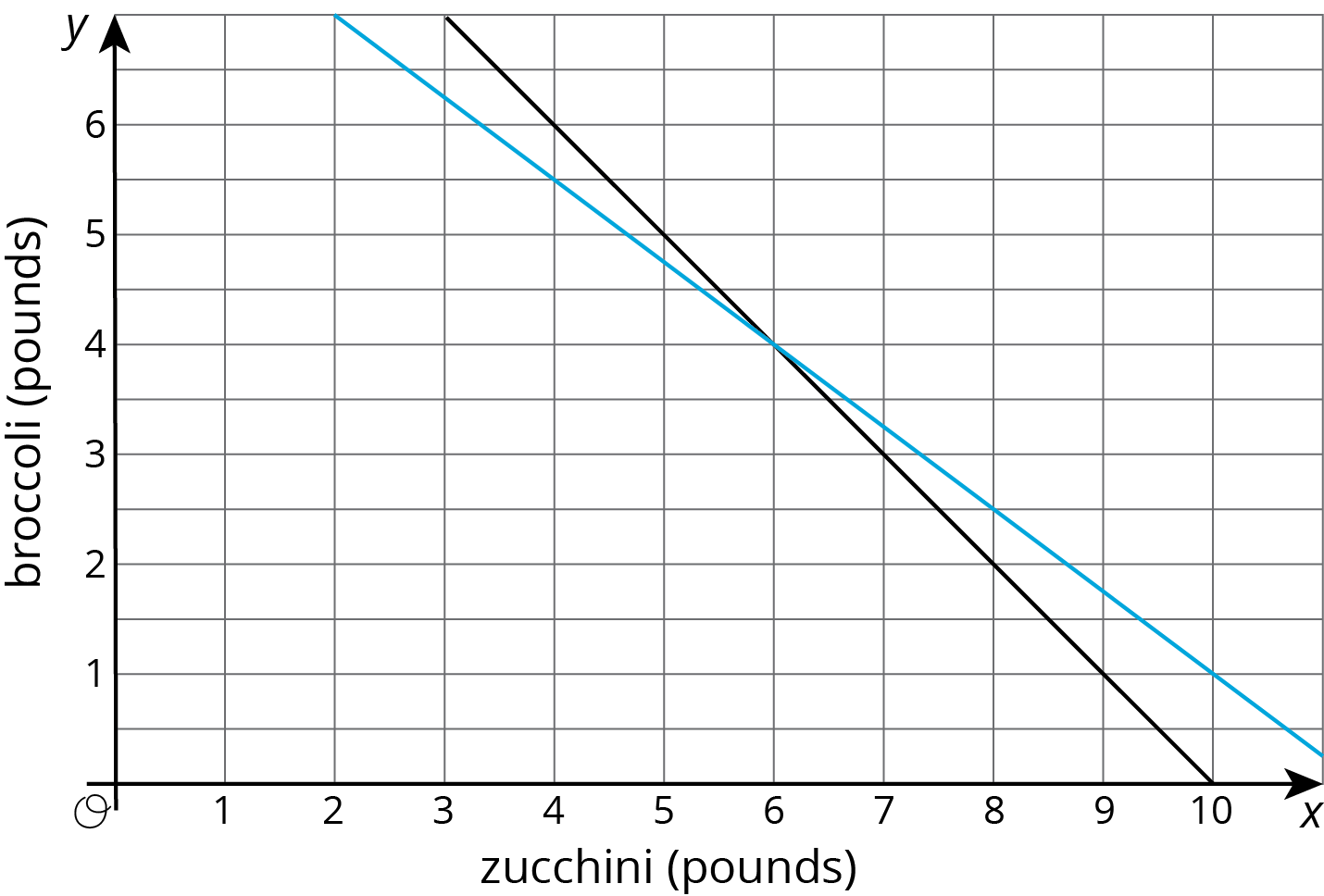
- Name one combination of veggies that weighs 10 pounds but does not cost $17.
- Name one combination of veggies that costs $17 but does not weigh 10 pounds.
- How many pounds each of zucchini and broccoli can Andre get so that he spends all $17 and gets 10 pounds of veggies?
Problem 4
The temperature in degrees Fahrenheit, \(F\), is related to the temperature in degrees Celsius, \(C\), by the equation \(\displaystyle F = \frac{9}{5}C + 32\)
-
In the Sahara desert, temperatures often reach 50 degrees Celsius. How many degrees Fahrenheit is this?
-
In parts of Alaska, the temperatures can reach -60 degrees Fahrenheit. How many degrees Celsius is this?
-
There is one temperature where the degrees Fahrenheit and degrees Celsius are the same, so that \(C=F\). Use the expression from the equation, where \(F\) is expressed in terms of \(C\), to solve for this temperature.