Lesson 7
Representations of Linear Relationships
Let’s write equations from real situations.
7.1: Estimation: Which Holds More?
Which glass will hold the most water? The least?

7.2: Rising Water Levels
Move the green circle to set the starting level of water to a value you or your teacher choose.
- What is the volume, \(V\), in the cylinder after you add:
- 3 objects?
- 7 objects?
- \(x\) objects? Explain your reasoning.
-
If you wanted to make the water reach the highest mark on the cylinder, how many objects would you need?
-
Plot and label points that show your measurements from the experiment.
-
Plot and label a point that shows the depth of the water before you added any objects.
-
The points should fall on a line. Use the Line tool to draw this line.
-
Compute the slope of the line using several different triangles. Does it matter which triangle you use to compute the slope? Why or why not?
-
The equation of the line in the experiment has two numbers and two variables. What physical quantities do the two numbers represent? What does \(V\) represent and what does \(x\) represent?
A situation is represented by the equation \(y = 5 +\frac12 x\).
-
Invent a story for this situation.
-
Graph the equation.
-
What do the \(\frac12\) and the 5 represent in your situation?
-
Where do you see the \(\frac12\) and 5 on the graph?
7.3: Calculate the Slope

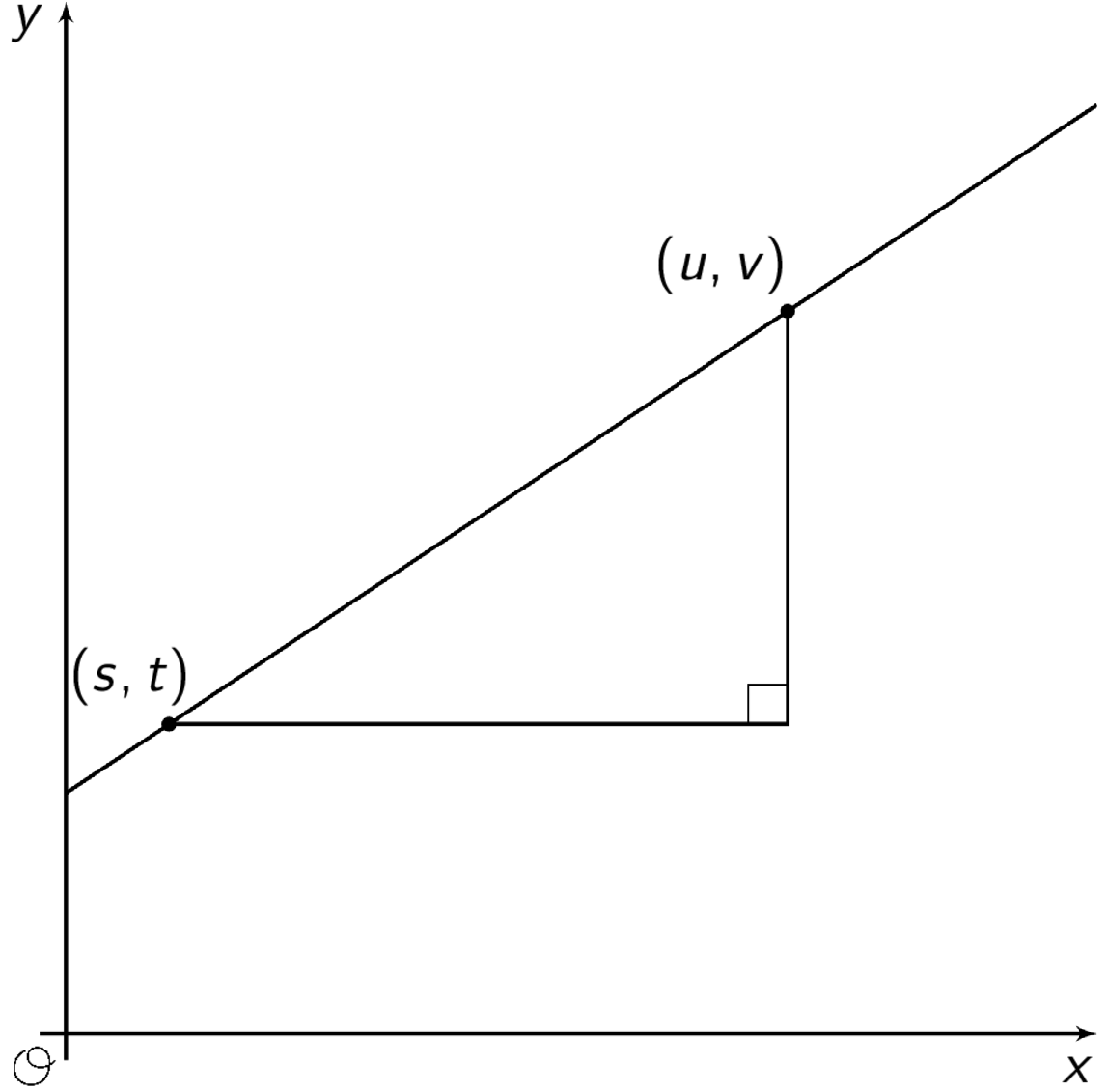
- For each graph, record:
vertical change horizontal change slope -
Describe a procedure for finding the slope between any two points on a line.
-
Write an expression for the slope of the line in the graph using the letters \(u, v, s,\) and \(t\).
Summary
Let's say we have a glass cylinder filled with 50 ml of water and a bunch of marbles that are 3 ml in volume. If we drop marbles into the cylinder one at a time, we can watch the height of the water increase by the same amount, 3 ml, for each one added. This constant rate of change means there is a linear relationship between the number of marbles and the height of the water. Add one marble, the water height goes up 3 ml. Add 2 marbles, the water height goes up 6 ml. Add \(x\) marbles, the water height goes up \(3x\) ml.
Reasoning this way, we can calculate that the height, \(y\), of the water for \(x\) marbles is \(y=3x+50\). Any linear relationships can be expressed in the form \(y=mx+b\) using just the rate of change, \(m\), and the initial amount, \(b\). The 3 represents the rate of change, or slope of the graph, and the 50 represents the initial amount, or vertical intercept of the graph. We'll learn about some more ways to think about this equation in future lessons.
Now what if we didn't have a description to use to figure out the slope and the vertical intercept? That's okay so long as we can find some points on the line! For the line graphed here, two of the points on the line are \((3,3)\) and \((9,5)\) and we can use these points to draw in a slope triangle as shown:

The slope of this line is the quotient of the length of the vertical side of the slope triangle and the length of the horizontal side of the slope triangle. So the slope, \(m\), is \(\frac{\text{vertical change}}{\text{horizontal change}}=\frac26=\frac13\). We can also see from the graph that the vertical intercept, \(b\), is 2. Putting these together, we can say that the equation for this line is \(y=\frac13x+2\).
Glossary Entries
- linear relationship
A linear relationship between two quantities means they are related like this: When one quantity changes by a certain amount, the other quantity always changes by a set amount. In a linear relationship, one quantity has a constant rate of change with respect to the other.
The relationship is called linear because its graph is a line.
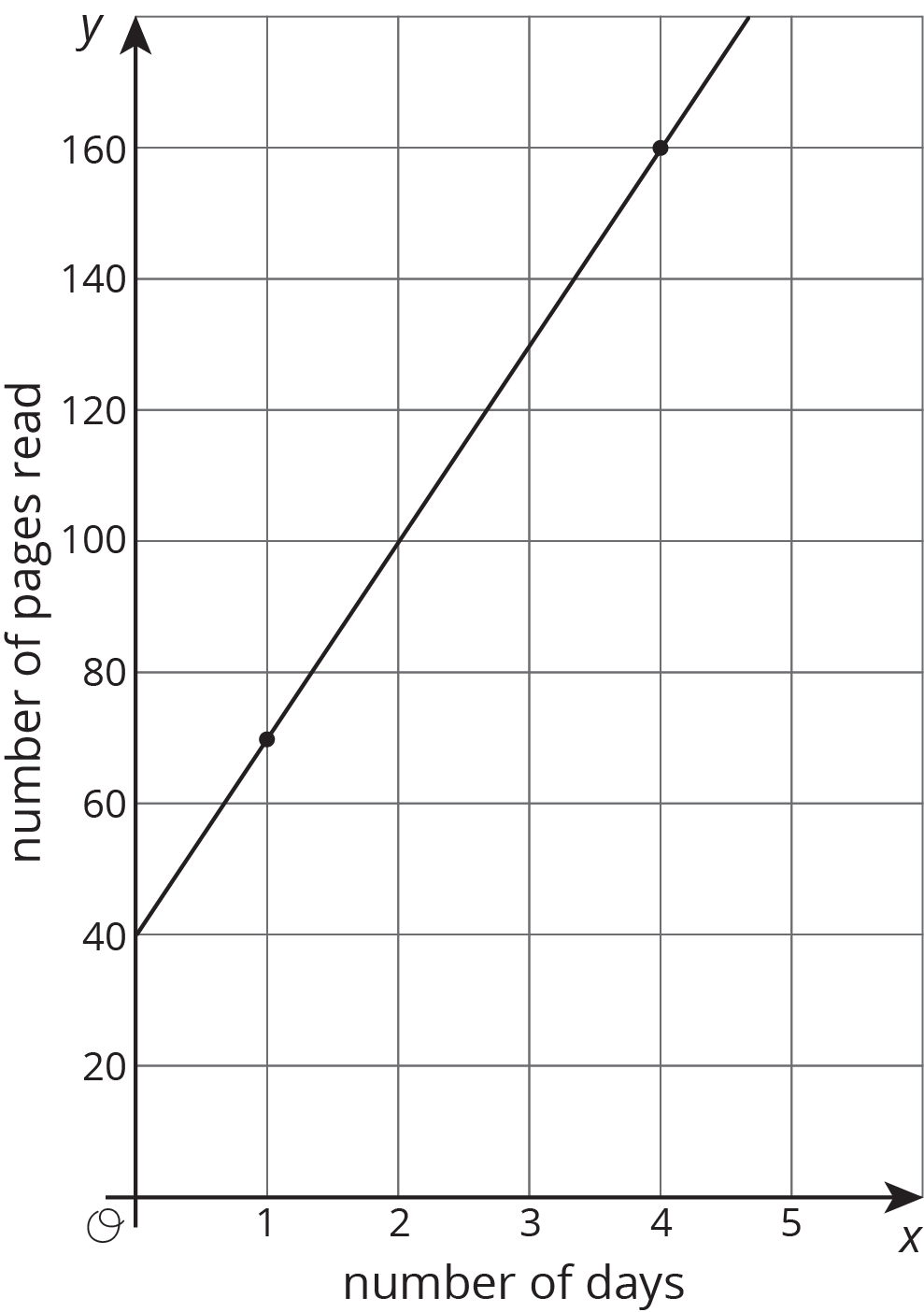
The graph shows a relationship between number of days and number of pages read.
When the number of days increases by 2, the number of pages read always increases by 60. The rate of change is constant, 30 pages per day, so the relationship is linear.
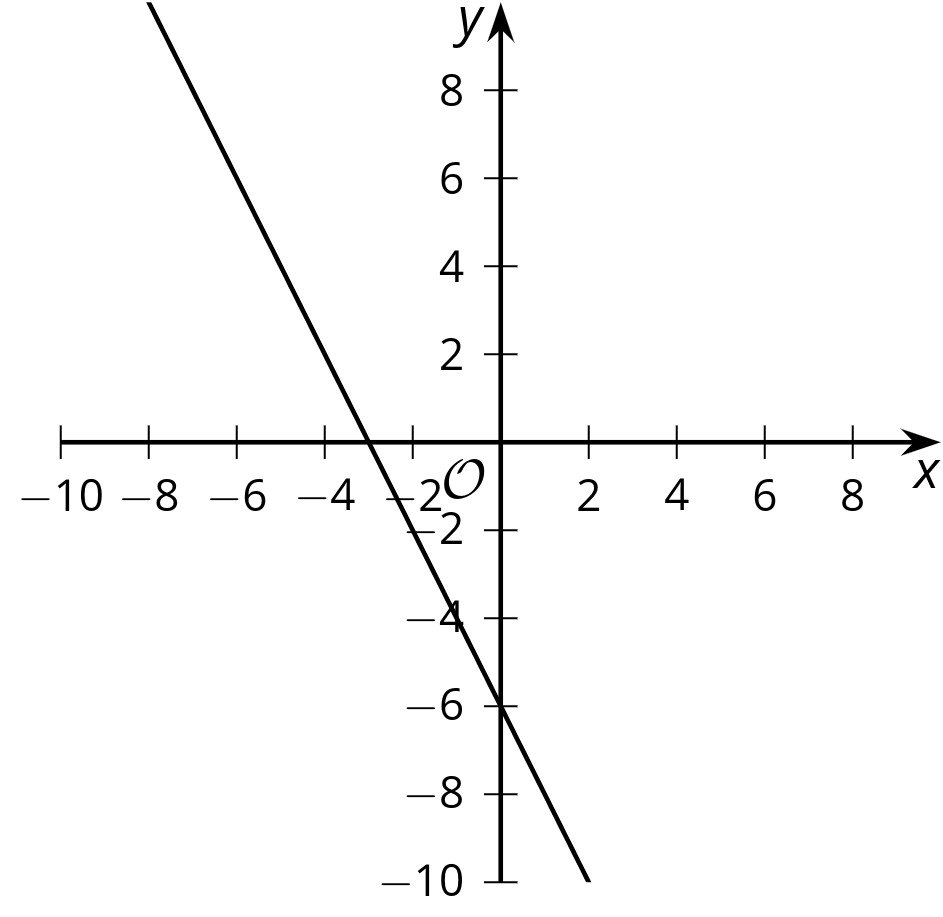
- vertical intercept
The vertical intercept is the point where the graph of a line crosses the vertical axis.
The vertical intercept of this line is \((0,\text-6)\) or just -6.