Lesson 9

More and Less than 1%

Let’s explore percentages smaller than 1%.

9.1: Number Talk: What Percentage?

Determine the percentage mentally.

10 is what percentage of 50?

5 is what percentage of 50?

1 is what percentage of 50?

17 is what percentage of 50?

9.2: Waiting Tables

During one waiter’s shift, he delivered appetizers, entrées, and desserts. What percentage of the dishes were desserts? appetizers? entrées? What do your percentages add up to?

9.3: Fractions of a Percent

  1. Find each percentage of 60. What do you notice about your answers?

    30% of 60

    3% of 60

    0.3% of 60

    0.03% of 60

  2. 20% of 5,000 is 1,000 and 21% of 5,000 is 1,050. Find each percentage of 5,000 and be prepared to explain your reasoning. If you get stuck, consider using the double number line diagram.

    1. 1% of 5,000

    2. 0.1% of 5,000

    3. 20.1% of 5,000

    4. 20.4% of 5,000

    A double number line with 12 tick marks.

  3. 15% of 80 is 12 and 16% of 80 is 12.8. Find each percentage of 80 and be prepared to explain your reasoning.

    1. 15.1% of 80

    2. 15.7% of 80



To make Sierpinski's triangle,

  • Start with an equilateral triangle. This is step 1.
  • Connect the midpoints of every side, and remove the middle triangle, leaving three smaller triangles. This is step 2.
  • Do the same to each of the remaining triangles. This is step 3.
  • Keep repeating this process.
3 steps of triangles.
  1. What percentage of the area of the original triangle is left after step 2? Step 3? Step 10? 
  2. At which step does the percentage first fall below 1%?

9.4: Population Growth

  1. The population of City A was approximately 243,000 people, and it increased by 8% in one year. What was the new population?

  2. The population of city B was approximately 7,150,000, and it increased by 0.8% in one year. What was the new population?

Summary

A percentage, such as 30%, is a rate per 100. To find 30% of a quantity, we multiply it by \(30\div 100\), or 0.3.

The same method works for percentages that are not whole numbers, like 7.8% or 2.5%. In the square, 2.5% of the area is shaded.

To find 2.5% of a quantity, we multiply it by \(2.5 \div 100\), or 0.025. For example, to calculate 2.5% interest on a bank balance of \$80, we multiply \((0.025)\boldcdot 80 = 2\), so the interest is \$2.

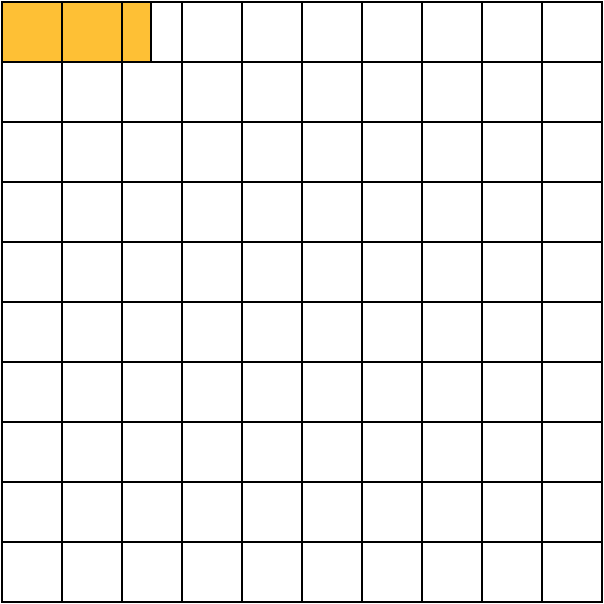
100 square grid with two and a half squares shaded in orange.

We can sometimes find percentages like 2.5% mentally by using convenient whole number percents. For example, 25% of 80 is one fourth of 80, which is 20. Since 2.5 is one tenth of 25, we know that 2.5% of 80 is one tenth of 20, which is 2.

Glossary Entries

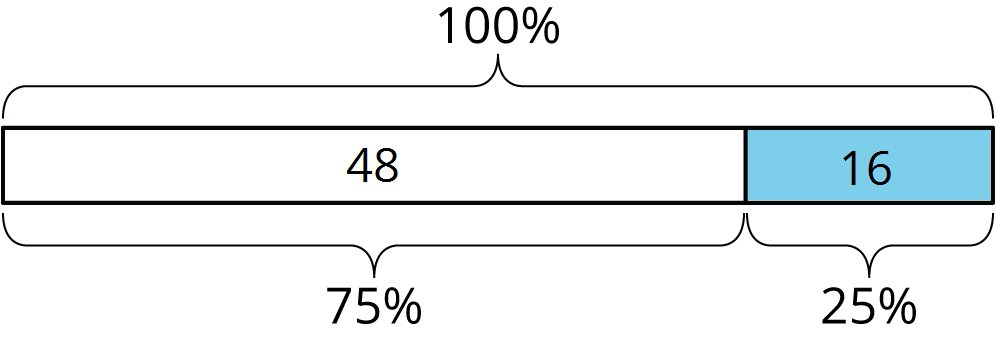
  • percentage decrease

    A percentage decrease tells how much a quantity went down, expressed as a percentage of the starting amount.

    For example, a store had 64 hats in stock on Friday. They had 48 hats left on Saturday. The amount went down by 16.

    This was a 25% decrease, because 16 is 25% of 64.

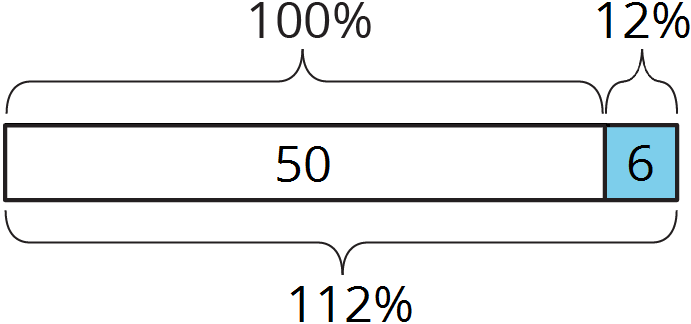
    a tape diagram
  • percentage increase

    A percentage increase tell how much a quantity went up, expressed as a percentage of the starting amount.

    For example, Elena had $50 in the bank on Monday. She had $56 on Tuesday. The amount went up by $6.

    This was a 12% increase, because 6 is 12% of 50. 

    a tape diagram