Lesson 8
Relating Area to Circumference
Let’s rearrange circles to calculate their areas.
8.1: Irrigating a Field
A circular field is set into a square with an 800 m side length. Estimate the field's area.
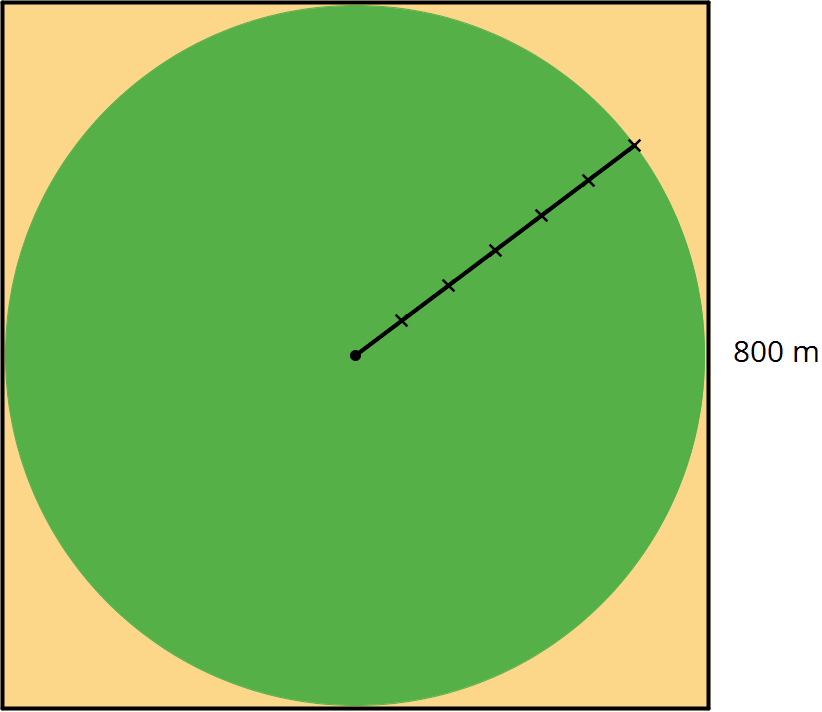
- About 5,000 m2
- About 50,000 m2
- About 500,000 m2
- About 5,000,000 m2
- About 50,000,000 m2
8.2: Making a Polygon out of a Circle
Your teacher will give you a circular object, a marker, and two pieces of paper of different colors.
Follow these instructions to create a visual display:
-
Using a thick marker, trace your circle in two separate places on the same piece of paper.
-
Cut out both circles, cutting around the marker line.
-
Fold and cut one of the circles into fourths.
-
Arrange the fourths so that straight sides are next to each other, but the curved edges are alternately on top and on bottom. Pause here so your teacher can review your work.
-
Fold and cut the fourths in half to make eighths. Arrange the eighths next to each other, like you did with the fourths.
-
If your pieces are still large enough, repeat the previous step to make sixteenths.
-
Glue the remaining circle and the new shape onto a piece of paper that is a different color.
After you finish gluing your shapes, answer the following questions.
-
How do the areas of the two shapes compare?
-
What polygon does the shape made of the circle pieces most resemble?
-
How could you find the area of this polygon?
8.3: Making Another Polygon out of a Circle
Imagine a circle made of rings that can bend but not stretch.

Watch the animation.
-
What polygon does the new shape resemble?
-
How does the area of the polygon compare to the area of the circle?
-
How can you find the area of the polygon?
-
Show, in detailed steps, how you could find the polygon’s area in terms of the circle’s measurements. Show your thinking. Organize it so it can be followed by others.
-
After you finish, trade papers with a partner and check each other’s work. If you disagree, work to reach an agreement. Discuss:
-
Do you agree or disagree with each step?
-
Is there a way they can make the explanation clearer?
-
-
Return your partner’s work, and revise your explanation based on the feedback you received.
8.4: Tiling a Table
Elena wants to tile the top of a circular table. The diameter of the table top is 28 inches. What is its area?
A box contains 20 square tiles that are 2 inches on each side. How many boxes of tiles will Elena need to tile the table?
Summary
If \(C\) is a circle’s circumference and \(r\) is its radius, then \(C=2\pi r\). The area of a circle can be found by taking the product of half the circumference and the radius.
If \(A\) is the area of the circle, this gives the equation:
\(A = \frac12 (2\pi r) \boldcdot r\)
This equation can be rewritten as:
\(A=\pi r^2\)
(Remember that when we have \(r \boldcdot r\) we can write \(r^2\) and we can say “\(r\) squared.”)
This means that if we know the radius, we can find the area. For example, if a circle has radius 10 cm, then the area is about \((3.14) \boldcdot 100\) which is 314 cm2.
If we know the diameter, we can figure out the radius, and then we can find the area. For example, if a circle has a diameter of 30 ft, then the radius is 15 ft, and the area is about \((3.14) \boldcdot 225\) which is approximately 707 ft2.
Glossary Entries
- area of a circle
If the radius of a circle is \(r\) units, then the area of the circle is \(\pi r^2\) square units.
For example, a circle has radius 3 inches. Its area is \(\pi 3^2\) square inches, or \(9\pi\) square inches, which is approximately 28.3 square inches.
- squared
We use the word squared to mean “to the second power.” This is because a square with side length \(s\) has an area of \(s \boldcdot s\), or \(s^2\).