Lesson 7
Areas under a Normal Curve
7.1: Find the Areas (5 minutes)
Warm-up
The mathematical purpose of this activity is for students to reason about the area under a normal curve using what they know about composition and decomposition of areas.
If students are using a table of values with \(z\)-scores for this lesson, this work will be essential to finding the desired areas in many cases.
Launch
Remind students that the phrase “the area under the curve” means the area between the \(x\)-axis and the curve.
Student Facing
The images show a normal curve with mean of 40 and standard deviation of 2.
The area under the curve to the left of 39 is 0.3085.

The area under the curve to the left of 43 is 0.9332.

Since it is a normal curve, we know that the total area under the curve is 1. Use the given areas to find the areas in question. Explain your reasoning for each.
- Find the area under the curve to the right of 39.
- Find the area under the curve between 39 and 43.
- Find the area under the curve to the left of 40.
- Find the area under the curve between 39 and 40.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is to make sure students can use the given areas to compose or decompose them to find additional areas. For each question, ask a student to explain how they reasoned about their answer. Highlight places where students used the symmetry of the distribution or cases where they could add or subtract known areas to find new areas.
7.2: Life of Lights (15 minutes)
Activity
The mathematical goal of this activity is for students to use the area under a normal curve to find the proportion of values in certain intervals. While the values in this activity are chosen to highlight the usual areas within 1, 2, and 3 standard deviations of the mean, it is not essential for students in this course to memorize those values.
Launch
Remind students that the phrase “area under the curve” means the area between the \(x\)-axis and the curve. Demonstrate how to use graphing technology to display the normal curve from the previous activity (a normal curve with mean of 40 and standard deviation of 2) and to find the area under the curve for values less than 39. See ggbm.at/w9tzezej.
If you are using the GeoGebra Probability Calculator, available in the toolkit or at geogebra.org/classic#probability, select Normal distribution and customize it by adjusting the mean and standard deviation. Choose the distribution you want to calculate from the three buttons labeled as shown below. Adjust the interval limits by either replacing their values in the formula, or by dragging them in the graph. The area under the curve is given by the calculated probability.
It may be helpful for students to open two GeoGebra windows—one for each of the situations in the problem statement.


Supports accessibility for: Organization; Conceptual processing; Attention
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
The life span of light bulbs is approximately normally distributed. Some statistics about life spans of two different types of light bulbs are listed.
- LED bulbs: mean = 2,300 days, standard deviation = 230 days
- incandescent bulbs: mean = 100 days, standard deviation = 10 days
To estimate the proportion of bulbs that burn out in a certain interval of time, use technology to find the area under the normal curve and above the appropriate interval.
- Estimate the proportion of LED bulbs that are expected to burn out before getting within 1 standard deviation of the mean (before 2,070 days).
- Estimate the proportion of incandescent bulbs that are expected to burn out before getting within 1 standard deviation of the mean (before 90 days).
- Estimate the proportion of LED bulbs that are expected to burn out after getting more than 1 standard deviation greater than the mean (after 2,530 days).
- Estimate the proportion of incandescent bulbs that are expected to burn out after getting more than 1 standard deviation greater than the mean (after 110 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 1 standard deviation less than the mean and 1 standard deviation greater than the mean (between 2,070 and 2,530 days).
- Estimate the proportion of incandescent bulbs expected to burn out in the interval between 1 standard deviation less than the mean and 1 standard deviation greater than the mean (between 90 and 110 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 2 standard deviations less than the mean and 2 standard deviations greater than the mean (between 1,840 and 2,760 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 1,900 days and 2,100 days.
- Estimate the proportion of incandescent bulbs that are expected to burn out in the interval between 107 and 118 days.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Remind students that the phrase “area under the curve” means the area between the \(x\)-axis and the curve. Demonstrate how to use graphing technology to display the normal curve from the previous activity (a normal curve with mean of 40 and standard deviation of 2) and to find the area under the curve for values less than 39.
Supports accessibility for: Organization; Conceptual processing; Attention
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
The life span of light bulbs is approximately normally distributed. Some statistics about life spans of two different types of light bulbs are listed.
- LED bulbs: mean: 2,300 days, standard deviation: 230 days
- incandescent bulbs: mean: 100 days, standard deviation: 10 days
To estimate the proportion of bulbs that burn out in a certain interval of time, use technology to find the area under the normal curve and above the appropriate interval.
- Estimate the proportion of LED bulbs that are expected to burn out before getting within 1 standard deviation of the mean (before 2,070 days).
- Estimate the proportion of incandescent bulbs that are expected to burn out before getting within 1 standard deviation of the mean (before 90 days).
- Estimate the proportion of LED bulbs that are expected to burn out after getting more than 1 standard deviation greater than the mean (after 2,530 days).
- Estimate the proportion of incandescent bulbs that are expected to burn out after getting more than 1 standard deviation greater than the mean (after 110 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 1 standard deviation less than the mean and 1 standard deviation greater than the mean (between 2,070 and 2,530 days).
- Estimate the proportion of incandescent bulbs expected to burn out in the interval between 1 standard deviation less than the mean and 1 standard deviation greater than the mean (between 90 and 110 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 2 standard deviations less than the mean and 2 standard deviations greater than the mean (between 1,840 and 2,760 days).
- Estimate the proportion of LED bulbs that are expected to burn out in the interval between 1,900 days and 2,100 days.
- Estimate the proportion of incandescent bulbs that are expected to burn out in the interval between 107 and 118 days.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students should be careful to use the correct mean and standard deviation for the type of bulb in the question. For students who struggle, ask them to more clearly identify the questions related to LED (or incandescent) bulbs to ensure they use the correct values in their technology.
Activity Synthesis
The goal of this discussion is for students to understand that a normal curve can be used to estimate the proportion of data that lie within a certain interval when the data is approximately normal. Ask,
- “Why is it important that we are told that the life spans are approximately normally distributed?” (If the data had a different type of distribution, modeling with a normal distribution would not accurately describe the situation. Compare this to modeling quadratic data with a line.)
- “Why are the answers for the first 4 questions the same?” (Since the normal curve is determined by the standard deviation and mean, the area to the left of the position one standard deviation below the mean is the same regardless of the values. Since the normal curve is symmetric, the area less than one standard deviation below the mean is equal to the area greater than one standard deviation above the mean.)
- “Since all normal curves have the same areas for the regions relative to the mean and number of standard deviations away, approximately what percentage of values are within 1 standard deviation of the mean? (About 68% are within 1 standard deviation of the mean.)
- “Approximately what percentage of values are within 2 standard deviations of the mean?” (About 95% are within 2 standard deviations of the mean.)
- “Approximately what percentage of values are within 3 standard deviations of the mean?” (About 99.7% are within 3 standard deviations of the mean.)
7.3: Waiting for a Waiter (15 minutes)
Optional activity
This activity is optional because finding an interval that fits a certain percentage of the data goes beyond the needs of this course. The mathematical purpose of this activity is to use the mean and standard deviation of a data set to fit it to a normal distribution and to estimate the interval given various proportions. Estimating an interval given various proportions is not required by the standards and students will not be assessed on questions like the ones in this activity, but these types of questions are included here so students have the opportunity to understand the concept of using the area under a normal curve to find the proportion of values in certain intervals more thoroughly.
Launch
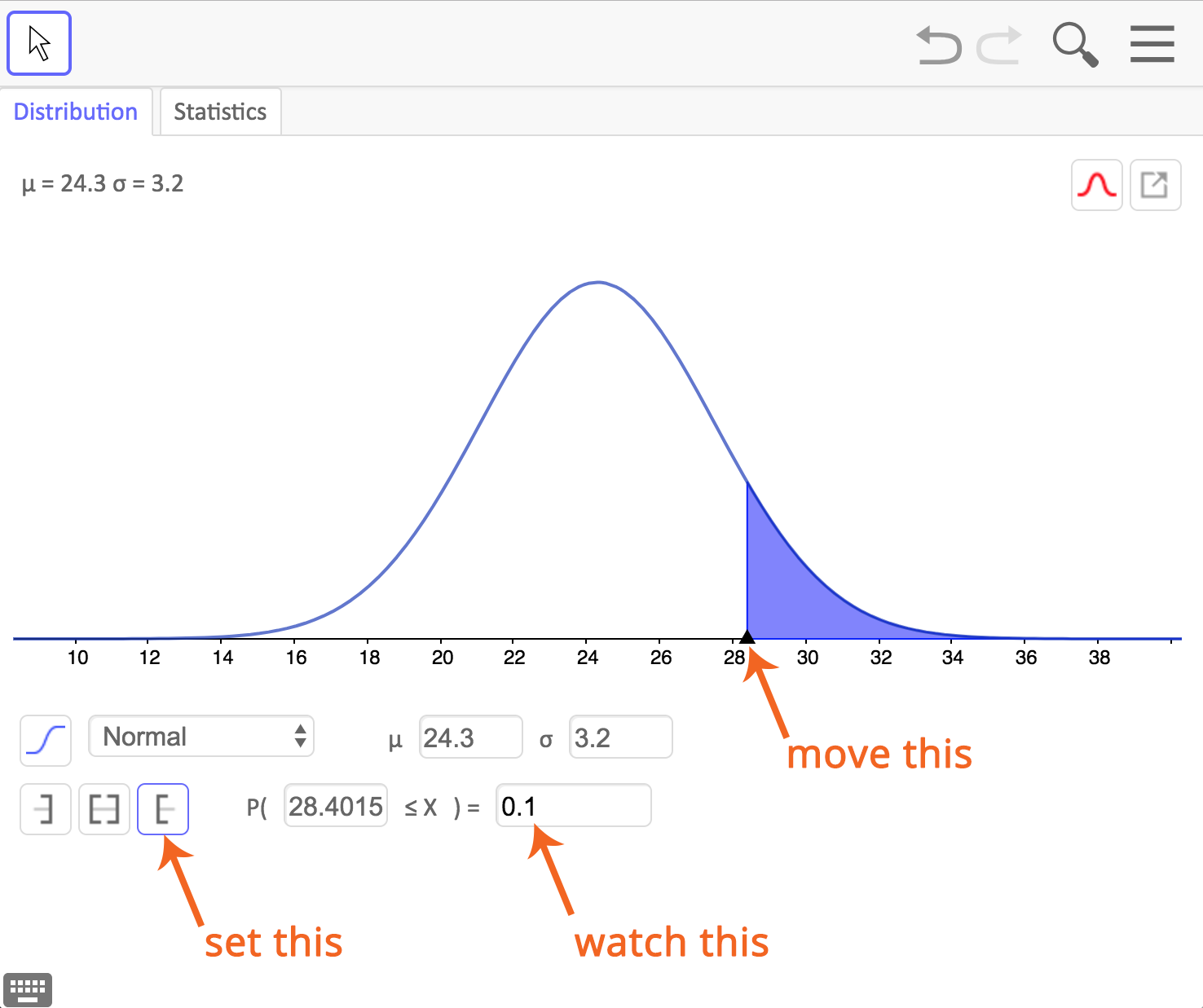
Tell students that they will use statistical technology to estimate the interval given various proportions. Open a new window in the GeoGebra Probabilty Calculator and set the values for the mean and standard deviation. Choose a closed interval, a left-bounded interval, or a right-bounded interval, depending on the context of the question. Move the black arrow on the \(x\)-axis until the probability shown in the box matches the condition of the question. The answer is given as the bound(s) for \(x \).
Student Facing
The wait times at a popular restaurant are approximately normally distributed. The mean wait time is 24.3 minutes with a standard deviation of 3.2 minutes.
Use technology to estimate the wait times for the described groups of diners.
- Describe the number of minutes diners have to wait if their wait times are in the longest 10% of wait times for diners at this restaurant.
- Describe the number of minutes diners have to wait if their wait times are in the shortest 15% of wait times for diners at this restaurant.
- To find the wait times for the middle 50% of wait times for diners:
- Draw an example of a normal distribution and shade approximately the middle 50% of the area under the curve.
- What percentage of the total area is unshaded to the left of the region you shaded? What value marks the line between the unshaded and shaded parts?
- What percentage of the total area is unshaded to the right of the region you shaded? What value marks the line between the unshaded and shaded parts?
- The shaded region is between which two values?
- The diners who have wait times in the middle 70% are between which two values?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Tell students that they will use statistical technology to estimate the interval given various proportions.
Student Facing
The wait times at a popular restaurant are approximately normally distributed. The mean wait time is 24.3 minutes with a standard deviation of 3.2 minutes.
Use technology to estimate the wait times for the described groups of diners.
- Describe the number of minutes diners have to wait if their wait times are in the longest 10% of wait times for diners at this restaurant.
- Describe the number of minutes diners have to wait if their wait times are in the shortest 15% of wait times for diners at this restaurant.
- To find the wait times for the middle 50% of wait times for diners:
- Draw an example of a normal distribution and shade approximately the middle 50% of the area under the curve.
- What percentage of the total area is unshaded to the left of the region you shaded? What value marks the line between the unshaded and shaded parts?
- What percentage of the total area is unshaded to the right of the region you shaded? What value marks the line between the unshaded and shaded parts?
- The shaded region is between which two values?
- The diners who have wait times in the middle 70% are between which two values?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A normal curve has a mean of 100 and a standard deviation of 10. For each value given, find two different regions that have approximately the given area and shade them in the graphs provided.
- 0.68
- 0.16
- 0.10
Area: 0.68

Area: 0.16

Area: 0.10

Area: 0.68

Area: 0.16

Area: 0.10

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to make connections between the area under the normal curve and the wait times at a restaurant. Here are some questions for discussion.
- “What percentage of diners wait within one standard deviation of the mean (from 21.1 to 27.5 minutes)?” (approximately 68%)
- “Approximately how long do the middle 95% of the diners wait?” (They wait within 2 standard deviations of the mean, from 17.9 to 30.7 minutes.)
- “A second restaurant has a longer mean wait time of 36.5 minutes and a standard deviation of 10.2 minutes. About how long do you think the middle 50% of diners wait at the second restaurant? How could you check your results? Explain your reasoning.” (I think they wait a little more than 26.3 minutes and a little less than 46.7 minutes. I know that about 68% of the diners wait between 26.3 and 46.7 minutes because that is within one standard deviation. I could get the actual times by modeling this with technology.)
- “Why is a normal curve a useful way to model wait times?” (The model is useful because the same model could be used to measure wait times at a variety of restaurants. Changing the mean wait time or the variability, as measured by the standard deviation, does not impact how the model is used.
Lesson Synthesis
Lesson Synthesis
Here are some questions for discussion.
- “In what ways can you investigate data by using the normal distribution as a model?” (A normal curve can allow you to estimate the proportion of values expected in certain intervals.)
- “Why are we finding the area under the curve?” (The area under the curve tells you the proportion of values in a certain interval.)
- “What proportion of values would you expect to be within one standard deviation of the mean?” (approximately 68%)
- “What proportion of values would you expect to be more than 2 standard deviations away from the mean?” (approximately 5%)
- “How does technology assist you in interpreting proportions using a normal curve?” (Technology allows me to find area under the curve for any value. Once I use the standard deviation and the mean to create the normal curve, I can estimate the proportion for any interval.)
7.4: Cool-down - Brown Bear, What Do You See? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The normal distribution can be used to estimate the proportion of values expected in a certain interval by finding the area under the normal curve and above the interval. Since the total area under a normal curve is 1, the area within any particular interval can be interpreted as the proportion of values that are in that interval.
To find the area, technology or reference tables can be used. When using technology, the system will need to know the mean and standard deviation for the data as well as the boundary values for the region where you want the area.
For example, the weights of large plastic building blocks are approximately normally distributed. The mean weight is 20 grams and the standard deviation is 0.7 grams. Let’s estimate the proportion of all plastic building blocks that weigh between 19.4 and 20.5 grams. This proportion is represented by the shaded area in the figure.

By adding all the information to a technological tool, we find that the proportion of values in this region is 0.5668 or 56.68%. This also means that, when selecting a building block at random, the probability of selecting a block with a weight between 19.4 and 20.5 grams is approximately 0.5668.