Lesson 15
Questioning Experimenting
15.1: Is It the Treatment? (10 minutes)
Warm-up
In this warm-up, students use their understanding of normal distributions to determine whether the difference is likely due to the random groupings or the treatment.
Student Facing
A scientist divides 30 strawberry plants into two groups at random. One group of 15 plants will represent the control group and is grown in standard greenhouse conditions. The second group of 15 plans will represent the treatment group and will grow under the same conditions except they are grown in a different type of soil. After 6 weeks, the total weight (in grams) of the strawberries are measured for each plant. The scientist then performs a randomized experiment to compare the groups.
The data are summarized by these statistics and histogram.
- Mean for the control group: 238.67 grams
- Mean for the group with different soil: 347.47 grams
- Mean of differences in means from randomized groupings: -0.540 grams
- Standard deviation of differences in means from randomized groupings: 29.83 grams

Is there evidence that the difference in means from the original groupings is due to the different soil or is it likely that the difference is due to the way the plants were grouped? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is to recall how the mean and standard deviation determine a normal distribution which can then be used to determine whether the observed difference in means is likely due to the random groupings or whether there is evidence that it is due to the treatment.
Ask students,
- "Why is it useful to know the standard deviation for the differences in means from randomized groupings?" (This number gives a sense of how spread out we expect the differences to get based on the groupings. It can be used to determine a normal distribution to determine how likely it is that the observed difference in means is due to chance groupings.)
- "How could the 'mean of differences in means from randomized groupings' be calculated using the original data?" (Redistribute the original data into two groups using a chance process to create new randomized groupings. Find the mean of each group and record the difference in means. Repeat the process many times to collect many differences in means for the groups. Find the mean of those recorded differences.)
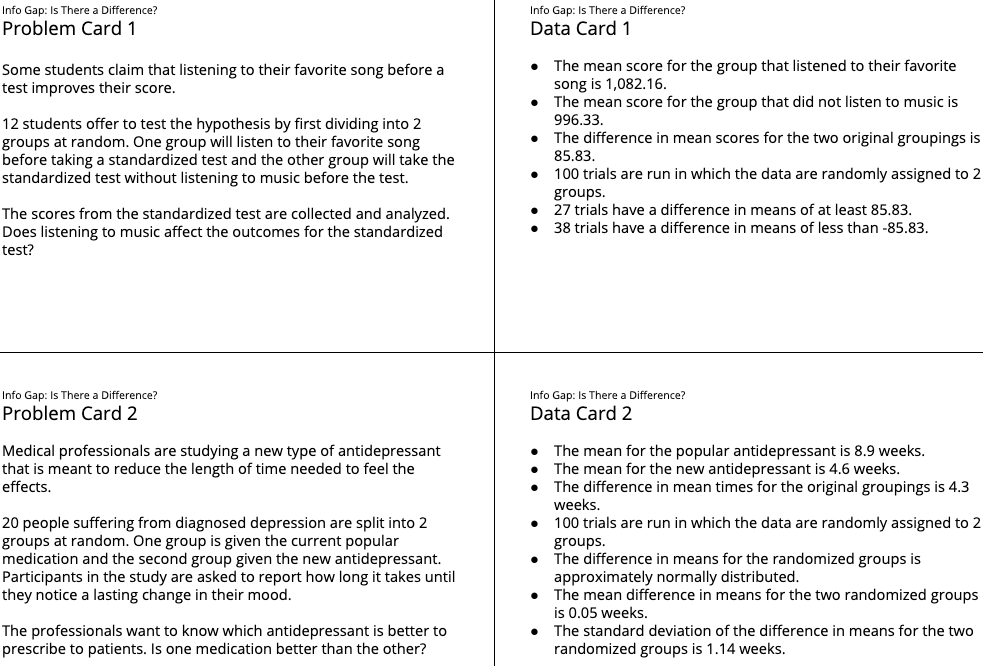
15.2: Info Gap: Is There a Difference? (25 minutes)
Activity
This info gap activity gives students an opportunity to determine and request the information needed to assess whether the results from an experiment are either significant or due to chance groupings.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Here is the text of the cards for reference and planning:
Launch
Tell students they will continue to examine data from experiments to determine if there is a significant difference in means or whether the difference is due to random groupings. Explain the info gap structure, and consider demonstrating the protocol if students are unfamiliar with it. Arrange students in groups of 2. In each group, distribute a problem card to one student and a data card to the other student. After reviewing their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Design Principle(s): Cultivate Conversation
Supports accessibility for: Memory; Organization
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the data card:
- Silently read the information on your card.
- Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
- Before telling your partner the information, ask “Why do you need to know (that piece of information)?”
- Read the problem card, and solve the problem independently.
- Share the data card, and discuss your reasoning.
If your teacher gives you the problem card:
- Silently read your card and think about what information you need to answer the question.
- Ask your partner for the specific information that you need.
- Explain to your partner how you are using the information to solve the problem.
- When you have enough information, share the problem card with your partner, and solve the problem independently.
- Read the data card, and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
After students have completed their work, share the correct answers and ask students to discuss the process of solving the problems. Here are some questions for discussion:
- “What questions did you ask that were helpful? Explain your reasoning.” (It was helpful to start by asking about the difference in means from the original groupings. That gave me a benchmark against which I could measure the information about the trials in which the data was randomly regrouped.)
- “Select a piece of information from one of the data cards. How could people collect or compute that information?” (After collecting the data from the experiments, find the mean of each group and subtract them.)
15.3: Using Tables for Normal Distribution Areas (10 minutes)
Optional activity
This activity is optional since it involves skills only needed in the absence of technology for finding areas under the normal curve.
In this activity, students explore the use of tables to find area under a normal curve bounded by certain values. Students are first introduced to z-scores and then use a table to find the area under the normal curve that is less than the value associated with that z-score.
Launch
Distribute the tables that show the areas under the standard normal curve based on z-scores. Demonstrate how to use the table to find the area for z-scores
- -1.96 (area of 0.0250)
- -0.50 (area of 0.3085)
- 1.65 (area of 0.9505)
Student Facing
A factory produces baseballs. The weights of the baseballs produced are approximately normally distributed with a mean weight of 145 grams and a standard deviation of 2 grams. Official rules require the balls to weigh between 142 and 149 grams.
Recall that the proportion of items in an interval of an approximately normally distributed situation is the same as the area under the normal curve. A table can be used to determine the area under a normal curve bounded by an interval.
First, the relevant values need to be converted to a z-score. A value's z-score represents the number of standard deviations it is above the mean. In the baseball example, the value 147 grams has a z-score of 1 since it is 1 standard deviation above the mean. The value 140 grams has a z-score of -2.5 since it is 2.5 standard deviations below the mean.
In general, a z-score can be found using
\(z = \frac{\text{value} - \text{mean}}{\text{standard deviation}}\)
- Find the z-score for 142 grams.
- Find the z-score for 149 grams.
- What value would have a z-score of 1.45?
-
The table gives the area under the normal curve that is less than the given value. Shade the region that is given by the table for the area related to 142 grams.
- Use the z-score for 142 grams and the table to find the area under the normal curve that is less than 142 grams.
-
Shade the region that is given by the table for the area related to 149 grams.
- Use the z-score for 149 grams and the table to find the area under the normal curve that is less than 149 grams.
- Use the two areas to find the area under the normal curve between 142 and 149 grams. Explain or show your reasoning.
- What proportion of the baseballs that the factory makes are within the official rules?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
There are 2 different distributions. Distribution A has a mean of 55 and a standard deviation of 8. Distribution B has a mean of 6 and a standard deviation of 1.6.
From distribution A, a person is interested in a value of 70 and from distribution B, the person is interested in a value of 10. How can z-scores be used to determine which is more relatively extreme?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may struggle to recognize the area given by the table using \(z\)-scores and think the area given is always the more extreme portion. Ask students to think about the value in the table and remind them that the entire area is 1, so if the value is greater than 0.5 it must be a region that takes up more than half of the area under the curve.
Activity Synthesis
The purpose of the discussion is for students to understand how to use a table to find areas under a normal curve.
Select students to share their solutions for all of their questions including their reasoning for the area under the normal curve between 142 and 149 grams.
Some additional questions for discussion:
- "Why are all the areas for positive z-scores greater than 0.5?" (Since positive z-scores represent values greater than the mean and the mean is the center of the distribution, at least half of the area is less than the value.)
- "Remember that the area under the entire normal curve is 1. How could you find the area of the region greater than a value that has a z-score of 0.95?" (The area under the normal curve and less than the value with a z-score of 0.95 is 0.8289. Since the entire area is 1, the area greater than that value is 0.1711 since \(1 - 0.8289 = 0.1711\).)
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
The purpose of the lesson is to have students practice asking questions needed to analyze data from an experiment. Consider asking,
- "What questions are the most important to ask about the data when determining whether there is evidence that the treatment for an experiment cause a difference in means for the original groups?" (What is the difference in means for the original group? After redistributing the data into groups at random, what proportion of these trials had differences in means that are more extreme than the original group?)
- "Why is it important to redistribute the data into groups at random many times?" (The more times the data is redistributed, the better we can understand what differences are possible and whether the original difference is likely or not.)
15.4: Cool-down - What Do You Need to Know? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
After collecting data from an experiment, it is important to analyze the data to determine whether there is evidence that the difference in means for the groups is due to the treatment or whether the difference might be explained by the random groupings. There are several things that an experimenter needs to know to determine the possible cause of the differences.
First, the difference in the means for the two groups is important to know. Then the difference can be compared to the differences in means collected from regrouping the data into groups at random. The proportion of differences in means that are more extreme than the original difference can help determine how likely it is that the original difference was due to the random grouping.
The proportion can be determined either from counting the actual number of differences that are more extreme or modeling the differences with a normal distribution.
