Lesson 9

What’s the Equation?

View Student Lesson

Problem 1

A party will have hexagonal tables placed together with space for one person on each open side:

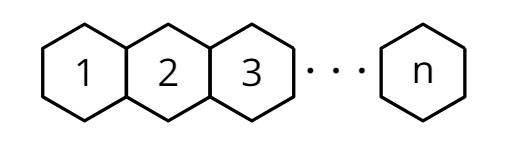
A paterrn of hexagons.
  1. Complete this table showing the number of people \(P(n)\) who can sit at \(n\) tables.
    \(n\) 1 2 3 4 5
    \(P(n)\) 6                        
  2. Describe how the number of people who can sit at the tables changes with each step.
  3. Explain why \(P(3.2)\) does not make sense in this scenario.
  4. Define \(P\) recursively and for the \(n^{\text{th}}\) term.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Diego is making a stack of pennies. He starts with 5 and then adds them 1 at at time. A penny is 1.52 mm thick.

  1. Complete the table with the height of the stack \(h(n)\), in mm, after \(n\) pennies have been added.
  2. Does \(h(1.52)\) make sense? Explain how you know.
\(n\) \(h(n)\)
0 \(7.6\)
1  
2  
3  

Solution

For access, consult one of our IM Certified Partners.

Problem 3

A piece of paper has an area of 80 square inches. A person cuts off \(\frac{1}{4}\) of the piece of paper. Then a second person cuts off \(\frac{1}{4}\) of the remaining paper. A third person cuts off \(\frac{1}{4}\) what is left, and so on.

  1. Complete the table where \(A(n)\) is the area, in square inches, of the remaining paper after the \(n^{\rm th}\) person cuts off their fraction.
  2. Define \(A\) for the \(n^{\text{th}}\) term.
  3. What is a reasonable domain for the function \(A\)? Explain how you know.
\(n\) \(A(n)\)
0 80
1  
2  
3  

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Here is the recursive definition of a sequence: \(f(1)=35, f(n) = f(n-1) - 8\) for \(n\ge2\).

  1. List the first 5 terms of the sequence.

  2. Graph the value of each term as a function of the term number.

Blank coordinate plane with grid, origin O. Horizontal axis from 0 to 6 by 1’s, labeled “term number”. Vertical axis from 0 to 50 by 5’s, labeled “value".

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 7.)

Problem 5

Here is a graph of sequence \(q\). Define \(q\) recursively using function notation.

Graph of a sequence Q on coordinate plane.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 6.)

Problem 6

Here is a recursive definition for a sequence \(f\): \(f(0) = 19, f(n) = f(n-1) - 6\) for \(n \geq 1\). The definition for the \(n^{\text{th}}\) term is \(f(n) = 19 - 6 \boldcdot n\) for \(n\ge0\).

  1. Explain how you know that these definitions represent the same sequence.
  2. Select a definition to calculate \(f(20)\), and explain why you chose it.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 8.)

Problem 7

An arithmetic sequence \(j\) starts 20, 16, . . . Explain how you would calculate the value of the 500th term.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 8.)