Lesson 17

The purpose of this warm-up is to get students to think more about what they mean by “light” and “heavy” to prepare for later activities that explore density.

Arrange students in groups of 2. After quiet work time, ask students to compare their responses to their partner’s and decide if they are both correct, even if they are different. Follow with a whole-class discussion.

Select students to share reasons that each might have more mass. It may be helpful to discuss how mass is measured to conclude that each, by definition, is the same mass. Then ask students to discuss what it means, specifically, when we say that feathers are lighter than steel, and how much volume a thousand kilograms of each substance might occupy.

Ask students to add this definition to their reference charts as you add it to the class reference chart:

The density of a substance is the mass of the substance per unit volume. That is, \(\text{density}=\frac{\text{mass}}{\text{volume}}\). (Definition)

density: 1 gram per cm³

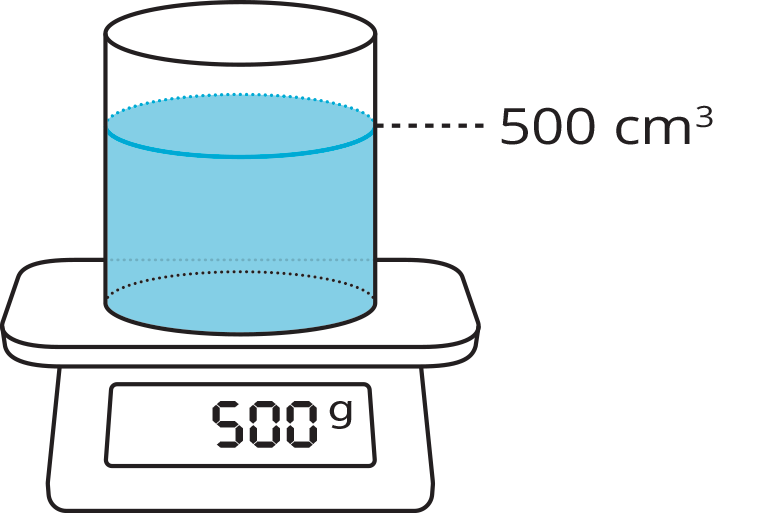
For example, a metal object whose mass is 150 kilograms with volume 1000 cubic centimeters has a density of \(\frac{150}{1000}\) or 0.15 kilograms per cubic centimeter. Each cubic centimeter of the metal contains 0.15 kilograms of mass.

Students use concepts of volume and unit conversion to enhance their understanding of density.

Tell students that 1 cubic meter is equal to 1,000,000 cubic centimeters and 1 kilogram is equal to 1,000 grams. Suggest that students pay careful attention to units as they work through this task.

Monitor for students who calculate the feather density in grams per cubic centimeter then convert to kilograms per cubic meter, and those who begin the task by converting the measurements to kilograms and cubic meters.

Students may calculate density in grams per cm³, then be unsure how to convert to kg per m³. Prompt them to either convert the measurements to cubic meters and kilograms prior to calculating density, or to use dimensional analysis to convert the density.

The purpose of the discussion is to draw out relationships between mass, volume, and density. Ask students:

• “How did you deal with the different units in this problem?” (If possible, select a student who calculated the feather density in grams per cm³ then converted to kg per m³, and another who converted the measurements to kilograms and cubic meters prior to calculating the density.)
• “How did you calculate the densities of each material?” (Divided the mass by the volume.)
• “How much space is 400 cubic meters? Would the feathers fill this room?” (A classroom of 30 feet by 30 feet by 12 feet has a volume of about 300 cubic meters.)
• “How much space is 0.124 cubic meters? Would the steel fit in the bed of a pickup truck?” (1,000 kg of steel would make a cube with edge length about 0.5 meters.)

This task presents a different way to think about density. Instead of considering mass per unit volume, students analyze animal population density. They use unit conversion and volume calculations to solve a problem. As students choose and track common units of measurement, they are attending to precision (MP6).

While students work, monitor for a variety of strategies such as:

• converting the density of 16 fish per 100 gallons of water to 0.16 fish per 1 gallon
• multiplying the tank’s volume in gallons by 16, then dividing by 100
• calculating that if 275 fish were used, the density would be about 14 fish per 100 gallons

Tell students that there are 7.48 gallons of water in 1 cubic foot.

Consider showing students pictures of the 82-foot tall cylindrical aquarium at the Radisson Blu hotel in Berlin, Germany.

The goal of the discussion is to highlight different ways to solve the problem. Ask students what the density of fish per 100 gallons would be if 275 fish were put in the tank, and what that means in this situation. Invite students to share how they approached rounding. For example, if the calculations show that 315.8 fish are needed, should we round up or down? Both answers can be supported.