Lesson 10

Solving Problems with Trigonometry

View Student Lesson

Problem 1

Technology required. Find the area of the isosceles trapezoid. 

Isosceles trapezoid. Bases 1 and 2 = 10 and 15 units. Base angles = 40 degrees 

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Technology required. The sun is 62 degrees above the horizon. A tree casts a shadow that is 12 feet long. How tall is the tree? 

Right triangle. Height = tree height. Bottom side = shadow formed from tree = 12 units. Hypotenuse from top of tree to end of shadow.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Technology required. A plane leaves the ground with an elevation angle of 6 degrees. The plane travels 10 miles horizontally.

  1. How high is the plane at the time? 
  2. What is the distance of the plane’s path? 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Technology required. Find the missing measurements.

Right triangle A B D. A B is 10 units and B D is 3 units. Angle B A D is labeled theta and angle A D B is labeled alpha.

Solution

For access, consult one of our IM Certified Partners.

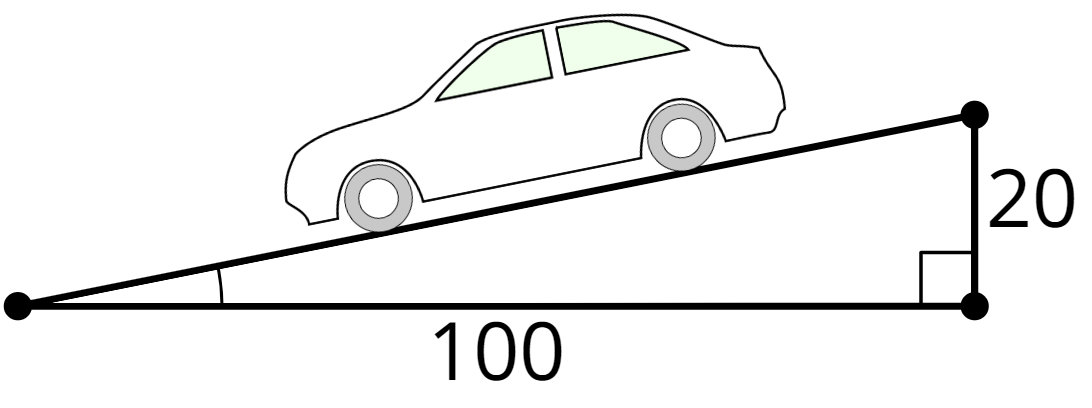
(From Unit 4, Lesson 9.)

Problem 5

Technology required. Ramps in a parking garage need to be both steep and safe. The maximum safe incline for a ramp is 8.5 degrees. 

Is this a safe ramp? Explain or show your reasoning.

Right triangle. Base 100 units, height 20 units. A car is drawn above the hypotenuse.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 9.)

Problem 6

Select all true equations. 

A:

\(\cos(37)=\sin(53)\)

B:

\(\tan(37)=\tan(53)\)

C:

\(\sin(37)=\cos(53)\)

D:

\(\sin(37)=\sin(53)\)

E:

\(\cos(\theta)=\sin(90-\theta)\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 8.)

Problem 7

Technology required. Clare is flying a kite. She gets tired, so she stakes the kite into the ground. The kite is on a string that is 30 ft long and makes a 27 degree angle with the ground. How high is the kite?

A:

30 ft

B:

13.6 ft

C:

26.7 ft

D:

15.3 ft

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 7.)

Problem 8

What is the length of the diagonal?

Square. Side length labeled 4.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 4, Lesson 2.)