Lesson 2
Scale of the Solar System
2.1: Solar Eclipse (5 minutes)
Warm-up
The context of an eclipse lends itself to diagrams of dilations. Students may or may not have intuition about an eclipse. Some may have observed an eclipse. Displaying pictures from a total solar eclipse in the launch will support students who are unfamiliar with the context. If the Moon were a different size or a different distance away, eclipses would look very different!
Launch
Make sure that students understand the context of an eclipse: that three celestial bodies are in a line, and because of their relative sizes and locations, one (in this case the moon) can cover the body behind it (in this case the sun) in such a way that the body is completely covered, or in such a way that a ring of light is visible around the eclipsing object. Showing images of a solar eclipse might help students understand the question better.
Student Facing
NOT TO SCALE

The diameter of the Sun is 1,391,000 km. The diameter of the Moon is 3,475 km. The distance from Earth to the Sun is 149,600,000 km.
How far would the Moon have to be from Earth for the Moon to appear the same size as the Sun?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share how they did their calculations.
“The average radius of the Moon’s orbit of Earth is 384,400 km. How well does reality match your calculations?” (The Moon’s actual orbit is very close to what I calculated. The Moon is a little farther away that it would need to be to appear the same size as the Sun, which means that you might see a little bit of the Sun peeking around the Moon during an eclipse.)
2.2: Shrinking the Solar System (30 minutes)
Optional activity
In this activity, students are building skills that will help them in mathematical modeling (MP4). Asking students to request needed information invites them to identify their variables and helps students recall how much information is needed to determine a scale factor and apply it to a known distance to find the scaled distance. This activity also allows students to practice calculating proportional relationships in a scale drawing. Monitor for students who:
- calculate using the equivalent ratios \(\frac{\text{Earth’s scaled diameter}}{\text{Earth’s actual diameter}}=\frac{\text{planet’s scaled diameter}}{\text{planet’s actual diameter}}\)
- calculate using the equivalent ratios \(\frac{\text{Earth’s scaled diameter}}{\text{planet’s scaled diameter}}=\frac{\text{Earth’s actual diameter}}{\text{planet’s actual diameter}}\)
- find a unit rate and scale up or down
- calculate by finding a scale factor and multiplying their planet’s actual diameter by that scale factor
Making spreadsheet technology available gives students an opportunity to choose appropriate tools strategically (MP5).
Launch
Tell students they will be making a scale drawing of the solar system, with accurately scaled sizes and distances from Earth for each planet. Display a circle with 2 cm diameter and explain that it will represent Earth. Show students where the class will (attempt to) display the scale drawing of the solar system. Explain that each group will be assigned a planet to draw and add to the scale drawing, at the appropriate distance.
Arrange students in groups of 3. Assign each group a planet. If there aren't enough groups to do all the planets pick some planets that are smaller than Earth and some that are larger than Earth. It is also fine to have multiple groups work on the same planet.
Pause the class after students have determined what information they need. Ask groups what information they need. Display the table and tell students this should be enough to figure out all the information they asked for. Note that any reference to the distance from a planet to Earth assumes that all planets are aligned perfectly in a line in order of orbital distance to the Sun.
| planet | average diameter (km) | average orbit radius (km) |
|---|---|---|
| Mercury | 4,879 | 57,900,000 |
| Venus | 12,104 | 108,200,000 |
| Earth | 12,756 | 149,600,000 |
| Mars | 6,792 | 227,900,000 |
| Jupiter | 142,984 | 778,600,000 |
| Saturn | 120,536 | 1,433,500,000 |
| Uranus | 51,118 | 2,872,500,000 |
| Neptune | 49,528 | 4,495,100,000 |
Supports accessibility for: Language; Social-emotional skills
Student Facing
The class is going to make a scale drawing of the planets in the solar system and their distances from Earth. Your teacher will assign you a planet to draw and place on the scale drawing. A circle with a diameter of 2 cm represents Earth.
- What information do you need in order to draw your planet and place it accurately on the class’s scale drawing?
- Your teacher will give you some information. Record the information here. Calculate any additional information you need.
- Draw the scale drawing of your planet on a separate sheet of blank paper. Label it with measurements. When you’re finished, place it the correct distance from Earth on the class’s scale drawing.
- You probably weren’t able to place your planet the correct scaled distance from Earth. Why not?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
- What has the greater quotient: the radius of Earth compared to the Sun or the radius of the Sun compared to the radius of the star Betelgeuse?
- If a circle of radius 6 cm represents the star Betelgeuse, how large would the Sun be? How large would the earth be?
- Draw the scale drawing of the Sun and Earth, or explain why you can't.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to use the information about orbital radius to find the planet’s distance from Earth encourage them to sketch the situation and label the information they know. (Image not to scale.)

Activity Synthesis
The key point of this discussion is to make sure students recall methods for finding unknown values in proportional relationships, and understand that the measurements in the scale drawing must all be scaled by the same scale factor.
Invite multiple students to share the calculations they did to find the size of their planet, given Earth’s scaled and actual size. First, select students to share who calculated using the equivalent ratios \(\frac{\text{Earth’s scaled diameter}}{\text{Earth’s actual diameter}}=\frac{\text{planet’s scaled diameter}}{\text{planet’s actual diameter}}\) or \(\frac{\text{Earth’s scaled diameter}}{\text{planet’s scaled diameter}}=\frac{\text{Earth’s actual diameter}}{\text{planet’s actual diameter}}\). Next, select students to share who calculated by finding a scale factor or unit rate. Invite students to share how the scale factor is included in all the calculations. (The quotients in the equivalent ratios are the same as the scale factor.)
Ask students:
- What units are your answers in? (Scaled values are in cm, actual values are in km.)
- Why didn't you need to convert from kilometers to centimeters? (The scale factor includes the units already.)
- How many times bigger is Earth than our 2 cm model? (A scale of \(2 \text{ cm}:12,\!756 \text{ km}\) is equivalent to a scale of \(1 \text{ cm}:6,\!378 \text{ km}\) which is equivalent to a scale of \(1 \text{ cm}:637,\!800,\!000 \text{ cm}\). So it's 637,800,000 times bigger!)
Design Principle(s): Support sense-making
2.3: Shrinking the Solar System, Take 2 (15 minutes)
Optional activity
This activity gives students extra practice with scale drawings and finding unknown values in proportional relationships. It also provides students with another chance to grapple with the size of the solar system and unit conversion. If students struggled to use an efficient method to find unknown values in proportional relationships, encourage students to use a strategy that a classmate demonstrated in the previous activity.
Making spreadsheet technology available gives students an opportunity to choose appropriate tools strategically (MP5).
Launch
Display the table and invite students to predict what size Earth would need to be for the scale drawing of the solar system to fit in the classroom.
| planet | average diameter (km) | average orbit radius (km) |
|---|---|---|
| Mercury | 4,879 | 57,900,000 |
| Venus | 12,104 | 108,200,000 |
| Earth | 12,756 | 149,600,000 |
| Mars | 6,792 | 227,900,000 |
| Jupiter | 142,984 | 778,600,000 |
| Saturn | 120,536 | 1,433,500,000 |
| Uranus | 51,118 | 2,872,500,000 |
| Neptune | 49,528 | 4,495,100,000 |
Keep students in the same groups they were in for the previous activity. Tell students to continue using the same planet as the previous activity.
Student Facing
Imagine that Earth is about the size of the period at the end of this sentence. That’s a diameter of 0.3 mm.
- How big is the scaled version of your planet now?
- How far from Earth is it?
- Can the scale drawing of the solar system fit in the classroom now?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The focus of the discussion is identifying efficient strategies for calculating the dimensions in a scale drawing. Select students who used different strategies to find the scale factor, and ask the class to think about why each strategy works. Then ask students to think about which strategy is the most efficient, and to come up with some tips for how to use the efficient strategy (or strategies).
Lesson Synthesis
Lesson Synthesis
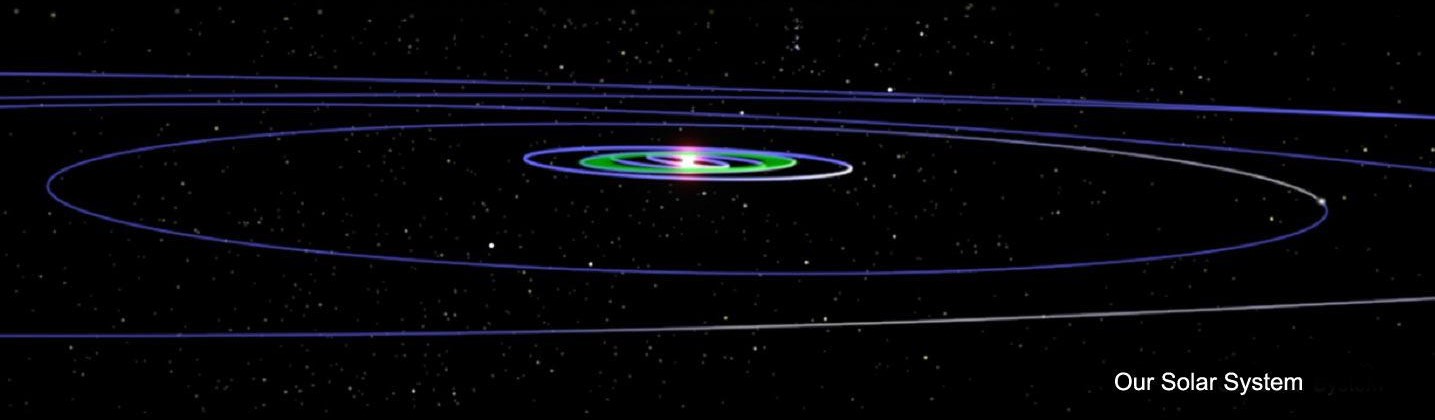
Discuss just how big the solar system is. These images might help students to understand the scale of the solar system. In one image they can see the planets to scale. Note that the Sun does not fit in the image and the distances are not to scale. In the other image the planets and orbits are both to scale, but the planets are so small most are invisible, and some orbits still extend beyond the image. This is hard to imagine. Performing an internet search for “solar system to scale video” and playing a video for all to see can help students get a better sense of the vastness of space.

2.4: Cool-down - Watching a Solar Eclipse on the Moon (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To make a scaled copy of this figure so that its new height is 3 cm instead of 8 cm, we could start calculating what the lengths of different parts of the figure would be. One way to calculate the measurements of the scaled copy is to multiply every length in the original figure by the scale factor \(\frac38\) to find the corresponding length in the scaled copy. For example, the radius of the head is 1.3 cm. \(1.3 \boldcdot \frac38 \approx 0.5\) so the radius of the scaled head is about 0.5 cm.

The length of segment \(AB\) is 2.4 cm. How long is segment \(A'B'\)? Instead of multiplying by the scale factor we could use equivalent ratios. Since \(\frac{A'B'}{AB}=\frac38\) then \(\frac{A'B'}{2.4}=\frac38\). So \(A'B'\) is 0.9 cm.
