Lesson 5
Building Quadratic Functions to Describe Situations (Part 1)
5.1: Notice and Wonder: An Interesting Numerical Pattern (5 minutes)
Warm-up
The purpose of this warm-up is to elicit the idea that the values in the table have a predictable pattern, which will be useful when students consider the context of a falling object in a later activity. While students may notice and wonder many things about this table, the patterns are the important discussion points, rather than trying to find a rule for the function. Because the rule is not easy to uncover, studying the numbers ahead of time should prove helpful as students analyze the function later.
This prompt gives students opportunities to see and make use of structure (MP7). The specific structure they might notice is all the \(y\) values are multiples of 16 and perfect squares. Some may notice the pattern is not linear and wonder whether it is quadratic.
Student Facing
Study the table. What do you notice? What do you wonder?
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \(y\) | 0 | 16 | 64 | 144 | 256 | 400 |
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share their observations and questions. Record and display them for all to see.
After all responses are recorded, tell students that they will investigate these values more closely in upcoming activities.
5.2: Falling from the Sky (15 minutes)
Activity
The motion of a falling object is commonly modeled with a quadratic function. This activity prompts students to build a very simple quadratic model using given time-distance data of a free-falling rock. By reasoning repeatedly about the values in the data, students notice regularity in the relationship between time and the vertical distance the object travels, which they then generalize as an expression with a squared variable (MP8). The work here prepares students to make sense of more complex quadratic functions later (that is, to model the motion of an object that is launched up and then returns to the ground).
Launch
Display the image of the falling object for all to see. Students will recognize the numbers from the warm-up. Invite students to make some other observations about the information. Ask questions such as:
- “What do you think the numbers tell us?”
- “Does the object fall the same distance every successive second? How do you know?”
Arrange students in groups of 2. Tell students to think quietly about the first question and share their thinking with a partner. Afterward, consider pausing for a brief discussion before proceeding to the second question.
Design Principle(s): Maximize meta-awareness; Cultivate conversation
Student Facing
A rock is dropped from the top floor of a 500-foot tall building. A camera captures the distance the rock traveled, in feet, after each second.
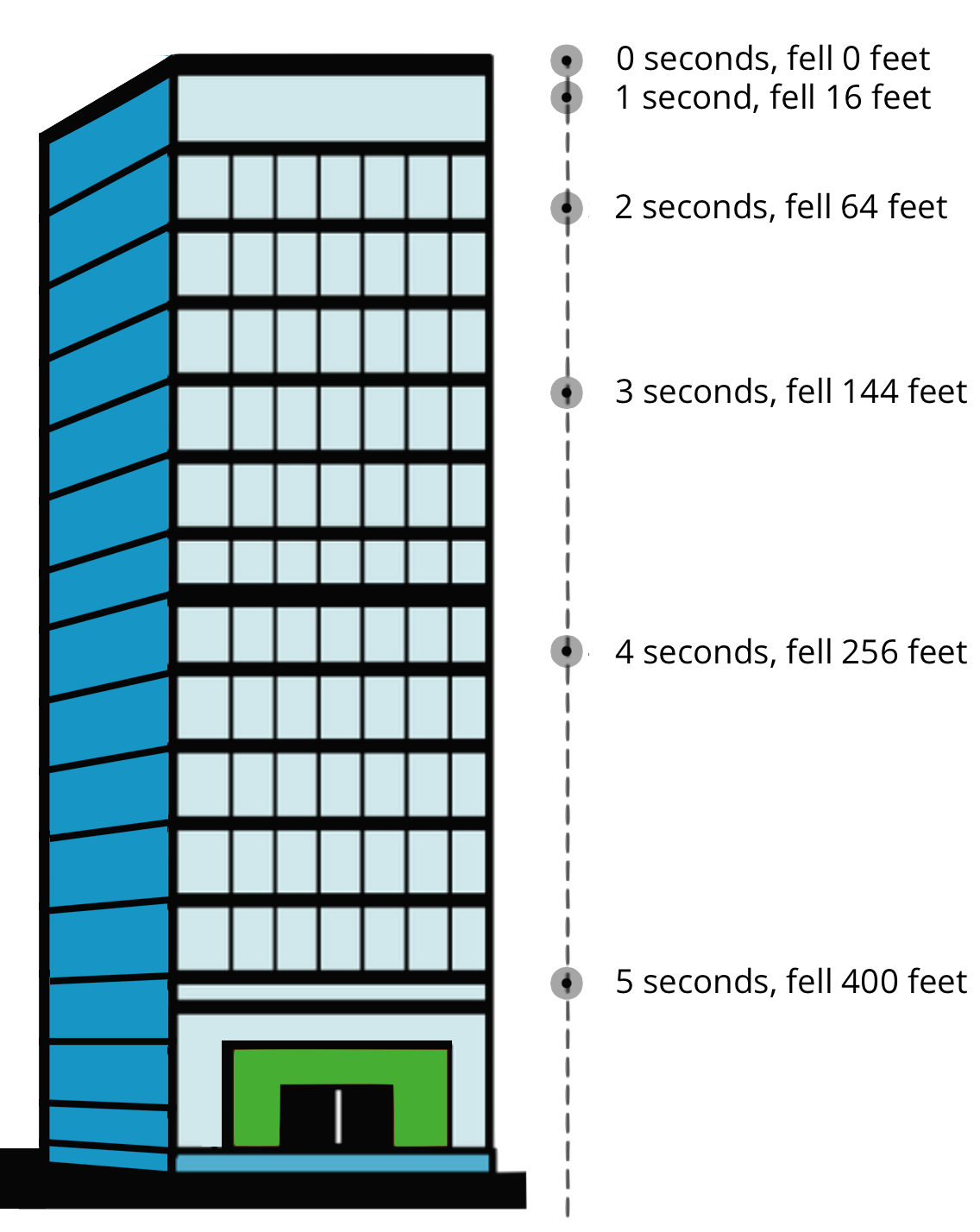
- How far will the rock have fallen after 6 seconds? Show your reasoning.
- Jada noticed that the distances fallen are all multiples of 16.
She wrote down:
\(\displaystyle \begin {align}16 &= 16 \boldcdot 1\\64 &= 16 \boldcdot 4\\144 &= 16 \boldcdot 9\\256 &= 16 \boldcdot 16\\400 &=16 \boldcdot 25 \end {align}\)
Then, she noticed that 1, 4, 9, 16, and 25 are \(1^2, 2^2, 3^2, 4^2\) and \(5^2\).- Use Jada’s observations to predict the distance fallen after 7 seconds. (Assume the building is tall enough that an object dropped from the top of it will continue falling for at least 7 seconds.) Show your reasoning.
- Write an equation for the function, with \(d\) representing the distance dropped after \(t\) seconds.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may question why the distances are positive when the rock is falling. In earlier grades, negative numbers represented on a vertical number line may have been associated with an arrow pointing down. Emphasize that the values shown in the picture measure how far the rock fell and not the direction it is falling.
Activity Synthesis
Discuss the equation students wrote for the last question. If not already mentioned by students, point out that the \(t^2\) suggests a quadratic relationship between elapsed time and the distance that a falling object travels. Ask students:
- “How do you know that the equation \(d=16t^2\) represents a function?” (For every input of time, there is a particular output.)
- “Suppose we want to know if the rock will travel 600 feet before 6 seconds have elapsed. How can we find out?” (Find the value of \(d\) when \(t\) is 6, which is \(16 \boldcdot 6^2\) or 576 feet.)
Explain to students that we only have a few data points to go by in this case, and the quadratic expression \(16t^2\) is a simplified model, but quadratic functions are generally used to model the movement of falling objects. We will see this expression appearing in some other contexts where gravity affects the quantities being studied.
5.3: Galileo and Gravity (15 minutes)
Activity
In this activity, students continue to explore how quadratic functions can model the movement of a falling object. They evaluate the function seen earlier (\(d=16t^2\)) at a non-integer input, and then build a new function to represent the distance from the ground of a falling object \(t\) seconds after it is dropped. To find a new expression that describes the height of the object, students reason repeatedly about the height of the object at different times and look for regularity in their reasoning (MP8).
The number 576 is chosen as the height (in feet) from which the object is dropped to make it more apparent for students that the values in the two tables (distance fallen and distance from ground) record distances measured from opposite ends. (Any value of \(16t^2\) at a whole-number \(t\) could work. In this case \(t=6\) is selected.)
Launch
Arrange students in groups of 2, and suggest that they check in with each other after trying each question. To facilitate peer discussion, consider displaying sentence stems or questions that students could use, such as:
- “Why do you think the object will have fallen that amount in 0.5 seconds?”
- “How do you think the values in the first table are changing? What about in the second table?”
- “How are the two tables alike? How are they different?”
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Galileo Galilei, an Italian scientist, and other medieval scholars studied the motion of free-falling objects. The law they discovered can be expressed by the equation \(d = 16 \boldcdot t^2\), which gives the distance fallen in feet, \(d\), as a function of time, \(t\), in seconds.
An object is dropped from a height of 576 feet.
- How far does it fall in 0.5 seconds?
-
To find out where the object is after the first few seconds after it was dropped, Elena and Diego created different tables.
Elena’s table:
time (seconds) distance fallen
(feet)0 0 1 16 2 64 3 4 \(t\) Diego’s table:
time (seconds) distance from the ground (feet) 0 576 1 560 2 512 3 4 \(t\) - How are the two tables are alike? How are they different?
- Complete Elena’s and Diego’s tables. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Galileo correctly observed that gravity causes objects to fall in a way where the distance fallen is a quadratic function of the time elapsed. He got a little carried away, however, and assumed that a hanging rope or chain could also be modeled by a quadratic function.
Here is a graph of such a shape (called a catenary) along with a table of approximate values.
| \(x\) | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 7.52 | 4.70 | 3.09 | 2.26 | 2 | 2.26 | 3.09 | 4.70 | 7.52 |
Show that an equation of the form \(y=ax^2+b\) cannot model this data well.

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
To help students make sense of the two functions, compare and contrast their representations (tables, equations, and graphs) and discuss the connections between them. Ask questions such as:
- “How did you complete the missing values in the first table?” (Substituting 3 and 4 for \(t\) in \(16t^2\) gives the distances fallen after 3 and 4 seconds.)
- “What about those in the second table?” (The distance from the ground is 576 minus the distance fallen, so we can use the values for \(t=3\) and \(t=4\) from the first table to calculate the values in the second table.)
- “Why do the values in the first table increase and those in the other table decrease?” (The distance from the top of the building increases as the object falls farther and farther away. The distance from the ground decreases as the object falls closer and closer to it.)
- “The expression representing the distance fallen shows \(16t^2\) and the other shows \(576 - 16t^2\). Why is that?” (In the first function, the distance fallen, measured from where the object is dropped, will always be positive. In the second function, what’s measured is the height from the ground, so the distance fallen needs to be subtracted from the height of the building.)
- “If we graph the two equations that represent distance fallen and distance from the ground over time, what would the graphs look like? Try sketching the graphs.”
Display graphs that represent the two functions and make sure students can interpret them. For example, they should see that the \(y\)-intercept of each graph corresponds to the starting value of each function before the object is dropped.
They should also notice that the difference in distance between successive seconds gets larger in both cases, hence the curving graphs. (If the differences were constant, the graphs would have been straight lines.)


Display the embedded applet for all to see. Ask students how the graph of the height of the object is related to the path that the object takes as it falls.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Lesson Synthesis
Lesson Synthesis
To highlight the key ideas from this lesson and the connections to earlier lessons, discuss questions such as:
- “We used two different functions to describe the movement of a falling object. One function measured the distance the object traveled from its starting point, and the other measured its distance from the ground. How are the representations of these functions alike and different?” (The equations both have \(16t^2\), but one is positive and the other negative. Their graphs are both curves, but one graph curves upward and the other downward. The values in one table shows increasing values and the other shows decreasing values, but they change by the same amounts from row to row.)
- “How are these functions like or unlike those representing visual patterns in earlier lessons?” (They can all be represented by quadratic expressions. The relationships between the step number and the number of squares or dots were easier to see. The relationships between time and distance are not as obvious.)
- “How are the graphs representing falling objects like or unlike those representing visual patterns?” (The graphs representing the patterns curved upward. They showed plotted points at whole-number inputs because non-whole-number steps would not make sense. In this lesson, we saw graphs that curved upward and downward. The graphs can be continuous, because we can measure the distances even when the number of seconds is fractional.)
5.4: Cool-down - Where Will It Be? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The distance traveled by a falling object in a given amount of time is an example of a quadratic function. Galileo is said to have dropped balls of different mass from the Leaning Tower of Pisa, which is about 190 feet tall, to show that they travel the same distance in the same time. In fact the equation \(d = 16t^2\) models the distance \(d\), in feet, that the cannonball falls after \(t\) seconds, no matter what its mass.
Because \(16 \boldcdot 4^2 = 256\), and the tower is only 190 feet tall, the cannonball hits the ground before 4 seconds.
Here is a table showing how far the cannonball has fallen over the first few seconds.
| time (seconds) | distance fallen (feet) |
|---|---|
| 0 | 0 |
| 1 | 16 |
| 2 | 64 |
| 3 | 144 |
Here are the time and distance pairs plotted on a coordinate plane:

Notice that the distance fallen is increasing each second. The average rate of change is increasing each second, which means that the cannonball is speeding up over time. This comes from the influence of gravity, which is represented by the quadratic expression \(16t^2\). It is the exponent 2 in that expression that makes it increase by larger and larger amounts.
Another way to study the change in the position of the cannonball is to look at its distance from the ground as a function of time.
Here is a table showing the distance from the ground in feet at 0, 1, 2, and 3 seconds.
| time (seconds) | distance from the ground (feet) |
|---|---|
| 0 | 190 |
| 1 | 174 |
| 2 | 126 |
| 3 | 46 |
Here are the time and distance pairs plotted on a coordinate plane:

The expression that defines the distance from the ground as a function of time is \(190 - 16t^2\). It tells us that the cannonball's distance from the ground is 190 feet before it is dropped and has decreased by \(16t^2\) when \(t\) seconds have passed.