Lesson 7
Spreadsheet Computations
Let's use spreadsheets as calculators.
Problem 1
Write a formula you could type into a spreadsheet to compute the value of each expression.
- \((19.2) \boldcdot 73\)
- \(1.1^{5}\)
- \(2.34 \div 5\)
- \(\frac{91}{7}\)
Problem 2
A long-distance runner jogs at a constant speed of 7 miles per hour for 45 minutes. Which spreadsheet formula would give the distance she traveled?
= 7 * 45
= 7 / 45
= 7 * (3 / 4)
= 7 / (3 / 4)
Problem 3
In a right triangle, the lengths of the sides that make a right angle are 3.4 meters and 5.6 meters. Select all the spreadsheet formulas that would give the area of this triangle.
= 3.4 * 5.6
= 3.4 * 5.6 * 2
= 3.4 * 5.6 / 2
= 3.4 * 5.6 * (1/2)
= (3.4 * 5.6) / 2
Problem 4
This spreadsheet should compute the total ounces of sparkling grape juice based on the number of batches, ounces of grape juice in a single batch, and ounces of sparkling water in a single batch.
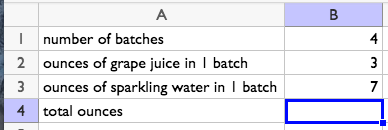
- Write a formula for cell B4 that uses the values in cells B1, B2, and B3, to compute the total ounces of sparkling grape juice.
- How would the output of the formula change if the value in cell B1 was changed to 10?
- What would change about the sparkling grape juice if the value in B3 was changed to 10?
Problem 5
The dot plot and the box plot represent the same distribution of data.


- How does the median change when the highest value, 5.2, is removed?
- How does the IQR change when the highest value, 5.2, is removed?
Problem 6
Describe the shape of the distribution shown in the histogram which displays the light output, in lumens, of various light sources.

Problem 7
The dot plot represents the distribution of the number of goals scored by a soccer team in 10 games.

- If possible, find the mean. If not possible, explain why not.
- If possible, find the median. If not possible, explain why not.
- Did the soccer team ever score exactly 3 goals in one of the games?