Lesson 3
Measure on a Map
Warm-up: Notice and Wonder: From Sea to Shining Sea (10 minutes)
Narrative
The purpose of this warm-up is to elicit ideas about length and distance on maps, which will be useful as students measure the distance between cities on maps throughout the lesson activities. While students may notice and wonder many things about the map and map features, comments about the distance between cities, states, or other features on the map are the most important.
If there is a range of background knowledge about maps, cities, and states, it may be helpful to focus the synthesis on sharing what students know about U.S. geography and map features that will be helpful when completing the first activity.
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Based on student responses, answer any questions to clarify the labels for cities and states.
- “What are things we could measure on a map?” (lines/borders of the states, the length or width of states, the distance between states and cities, the distance from one side of the country to the other)
Activity 1: Measure on the Map (20 minutes)
Narrative
The purpose of this activity is for students to measure lengths to the nearest centimeter and to find the total distance each student moves on the map. The synthesis focuses on sharing student methods for addition using properties of operations and the sums they know from memory. When students measure and represent the trips with equations and find the total distance on the map, they reason abstractly and quantitatively (MP2).
Depending on students’ experiences with maps and U.S. geography, it may be helpful to pause during the activity to share the strategies students use for locating cities and states on the map.
Supports accessibility for: Attention, Organization
Required Materials
Launch
- Groups of 2
- Give each student a ruler and a map.
Activity
- “Use the map and your tools to measure the distances each student travels.”
- 15 minutes: partner work time
- As students find the total length for each trip, monitor for students who:
- explain or show methods that create equivalent, but easier or known sums
- explain methods based on using known facts
Student Facing
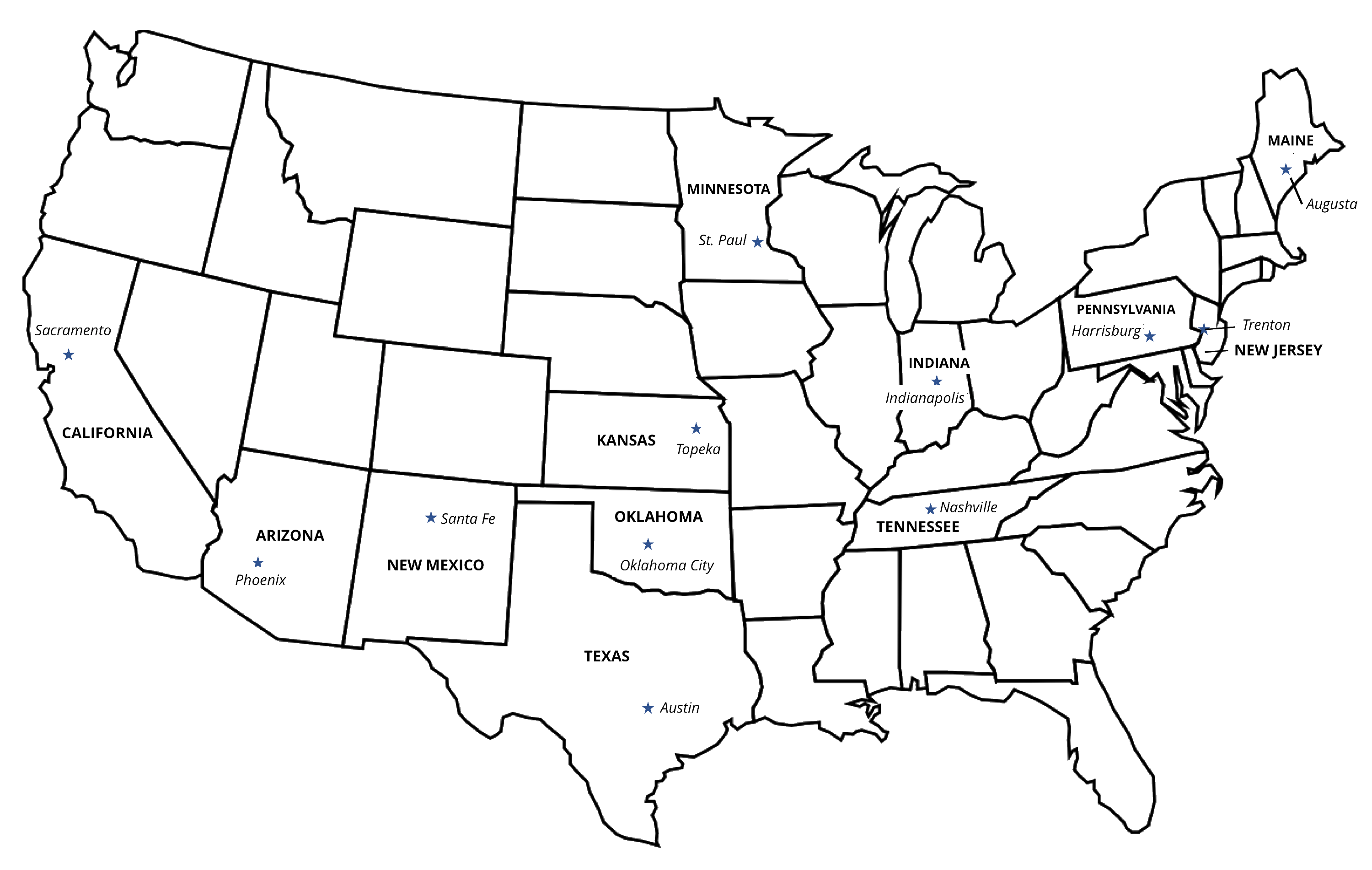
Draw a line to represent the distance between cities on the map. Then measure the length in centimeters.
-
Noah started in Trenton, New Jersey.
- First, he traveled to Harrisburg, Pennsylvania. _____ cm
- Next, he traveled from Harrisburg to Indianapolis, Indiana. _____ cm
- Last, he traveled from Indianapolis to St. Paul, Minnesota. _____ cm
-
Diego started in Sacramento, California.
- First, he traveled to Phoenix, Arizona. _____ cm
- Next, he traveled from Phoenix to Santa Fe, New Mexico. _____ cm
- Last, he traveled from Santa Fe to Topeka, Kansas. _____ cm
-
Lin started in Austin, Texas.
- First, she traveled to Oklahoma City, Oklahoma. _____ cm
- Next, she traveled from Oklahoma City to Nashville, Tennessee. _____ cm
- Last, she traveled from Nashville to Augusta, Maine. _____ cm
-
Find the total length of each student’s trip. Represent the total with an equation.
- Lin’s total
- Diego’s total
- Noah’s total
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite 1–2 previously identified students to share their equation for Diego’s total.
- Consider asking:
- “How did you find Diego’s total? Why did you make that decision?”
- Invite 1–2 previously identified students to share their equation for Lin’s total.
- Consider asking:
- “How did you find Lin’s total? Why did you make that decision?”
Activity 2: How Much Longer? (15 minutes)
Narrative
The purpose of this activity is for students to compare the lengths they measured in the previous activity. Students are encouraged to share and compare strategies they use for finding the unknown length.
As students compare lengths, ask them about the methods they are using. In particular, identify students who are using the following methods for finding difference:
- making equivalent, but easier sums or differences (making 10)
- using known facts (changing equations to make known facts, using relationship between addition and subtraction, etc.)
Advances: Conversing, Reading
Launch
- Groups of 2
Activity
- “Now answer the questions about the length of the path the students traveled on the map. Be ready to share your thinking with your partner.”
- 4 minute: independent work time
- 2 minutes: partner discussion
- As students find the difference of Lin's and Noah’s trips, monitor for students who:
- use a known addition fact
- explain or show counting up or back to make ten (\(9 + 1 = 10\), \(10 + 7 = 17\), \(1 + 7 = 8\))
- explain or show methods that create equivalent, but easier or known differences (add 1 to 17 and 9 to create \(18 - 10 = 8\))
Student Facing
Use your map and the stories from the previous activity to answer the questions. Represent each story with an equation with a symbol for the unknown length.
- How much shorter is the total length of Diego’s trip than the total length of Lin’s trip?
- How much longer is the total length of Diego’s trip than the total length of Noah’s trip?
- How much shorter is the total length of Noah’s trip than the total length of Lin’s trip?
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students add the lengths of the student trips rather than finding the difference, consider asking:
- “Who’s trip is longer? Is their trip a little longer or much longer?”
- “How could you use a diagram to show the difference between the lengths of their trips?"
Activity Synthesis
-
Invite previously identified students to share their equation that shows the difference of Lin's and Noah's trips, or display: \(17 - 9 = {?}\)
- “How could you use an addition fact that you know to find the unknown?” (\(9 + 8 = 17\))
- “What is another way you could make this an easier difference to find?” (You could think about making a 10. Add 1 to the 9 and think about how many more you would need to get to 17. Add 1 to both numbers and subtract 10.)
- “Using addition facts you know and looking for ways to make easier expressions are two good methods for finding sums and differences accurately and quickly.”
Lesson Synthesis
Lesson Synthesis
“Share your work from the cool-down.”
1 minute: partner discussion
Share responses.
Cool-down: Practice Facts (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.