Lesson 2
Partners Make Pairs
Warm-up: Which One Doesn’t Belong: Laundry Day (10 minutes)
Narrative
Launch
- Groups of 2
- Display image.
- “Pick one that doesn’t belong. Be ready to share why it doesn’t belong.”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 2–3 minutes: partner discussion
- Record responses.
Student Facing
Which one doesn’t belong?




Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How does each image show pairs of socks?” (Sample responses: A shows 4 pairs side-by-side, but they don’t match. B shows 3 pairs of socks that are the same color and right next to each other. C shows socks in 2 rows. The matching pairs are above and below each other. D shows matching pairs side-by-side.)
Activity 1: Pair Up (20 minutes)
Narrative
The purpose of this activity is for students to separate objects into groups of 2 and identify numbers of objects that can be split into pairs with “no leftovers” and numbers of objects that can be split into pairs with “one leftover.” In the synthesis, create a t-chart with students that lists the numbers that belong to each category. Students share what they notice and wonder about each group of numbers. Save the t-chart for use in the lesson synthesis.
When recording student responses in the synthesis, record how students counted to find the total number of counters by drawing pairs in rows (see activity synthesis). This helps students see the groups of 2 and prepares them for analyzing arrays in future lessons.
This activity uses MLR8 Discussion Supports. Advances: speaking.
Required Materials
Materials to Gather
Required Preparation
- Each group of 2 needs a container of 4 to 15 counters.
- Create a t-chart on a large piece of chart paper to display in the activity synthesis.
- Use “Making Pairs” as the title.
- Label the t-chart with “no leftovers” and “one leftover” as the categories.
Launch
- Groups of 2
- Give each group a bag of counters.
Activity
- “Work with your partner to make as many pairs of 1 red and 1 yellow counter that you can. Represent your counters with a drawing or symbols in the first column.”
- “Record the total amount of counters and the number of counters left over, after you have made pairs.”
- “When you finish pairing the counters in one bag, pack up the counters and trade with another group.”
- 10 minutes: partner work time
Student Facing
Make pairs with 1 yellow counter and 1 red counter.
my counters

total counters

leftover counters
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
- “How does your arrangement show a pair of counters that has 1 red and 1 yellow?”
- “How could you rearrange your counters to show pairs?”
Activity Synthesis
- Display t-chart labeled “Making Pairs” with “no leftovers” and “one leftover” as the categories.
- Invite students to share a total amount and whether they made pairs with no leftovers or pairs with a leftover.
- Record the total on the chart.
- “How did you count the counters to find the total?” (I counted each pair by 2.)
- Represent how the student counted by drawing dots in rows. If students count by 2, represent this by drawing two dots at a time and count by 2.
- For example:
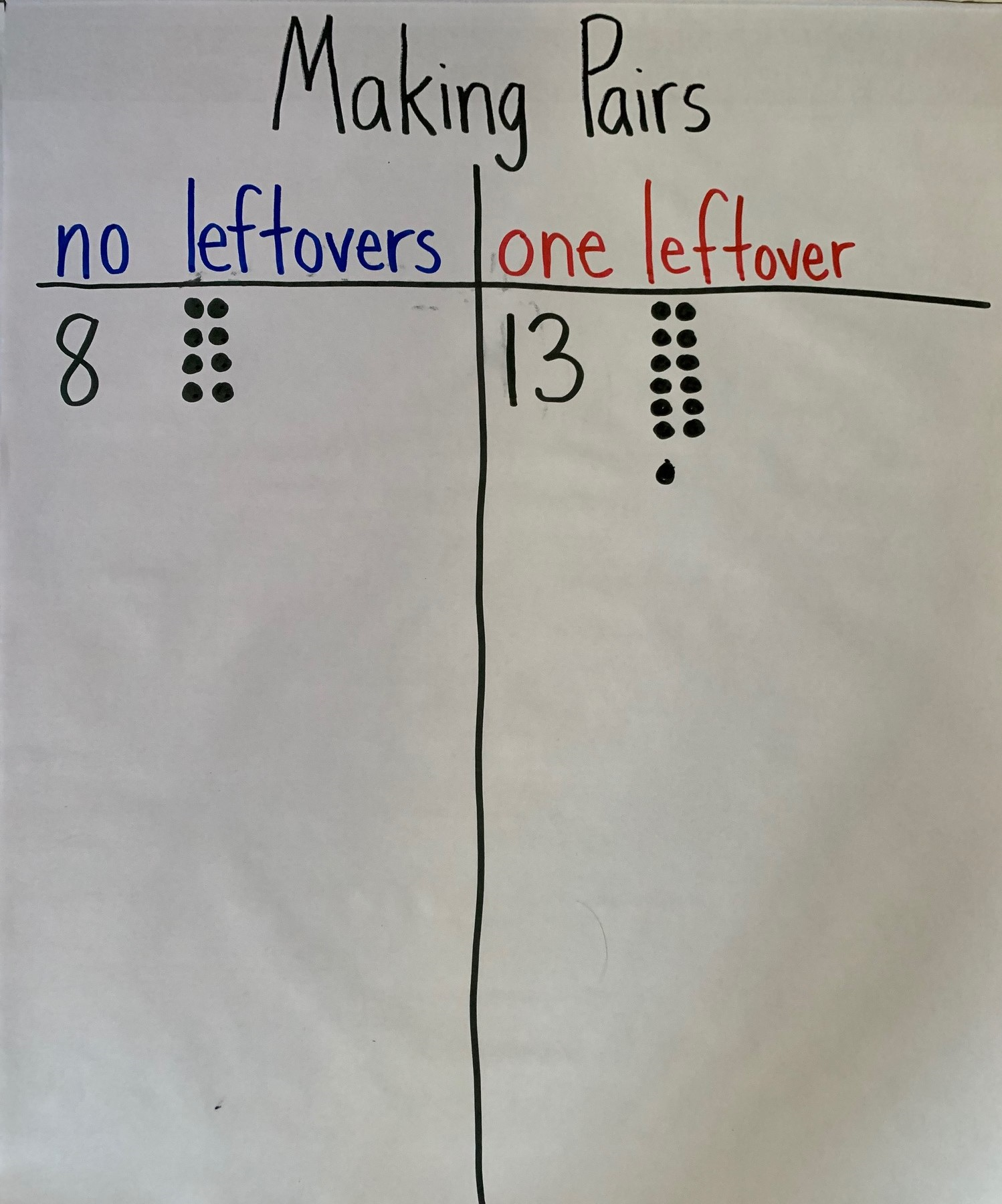
- For example:
- “Look at the numbers in each group. What do you notice? What do you wonder?” (All of the numbers show pairs. The numbers in the leftover group have only 1 leftover, the rest make pairs. I wonder what other numbers go in these groups. I wonder if these are the same numbers we found had 1 leftover yesterday.)
- Before students share, remind students to use words such as pairs, equal groups, and leftovers.
- 1 minute: quiet think time
- 1-2 minutes: partner discussion
- Share responses.
- If needed, “How many leftovers did each number have?”
Activity 2: Are You Feeling Left Out? (15 minutes)
Narrative
The purpose of this activity is for students to determine whether a group of people (16–20) can be organized into groups of 2 without any person left alone or any groups of 3. They begin to reason about whether a group of objects is even or odd by using what they know about counting or adding by 2 (MP7, MP8). Students should be given access to counters, but may use other representations, including equations.
Supports accessibility for: Conceptual Processing, Social-Emotional Functioning
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to connecting cubes or counters.
- Have students pair up to find a new partner or line up in pairs.
- “Does everyone have a partner?”
- “When we need a partner for an activity, are we always able to have only groups of 2?” (No. When ___ was absent, we had to make a group of 3.)
Activity
- “Let’s show whether all students in different class sizes can be paired up to make only groups of 2.”
- “Do the first question on your own.”
- 3 minutes: independent work time
- “Compare your thinking with your partner. Then answer numbers 2 and 3 together.”
- 8 minutes: partner work time
- Monitor for different ways students show pairs for 19 students to share in the synthesis.
Student Facing
Show your thinking using diagrams, symbols, or other representations. Use cubes or counters if it helps.
- There are 18 students in Clare’s class today. They will work in pairs. Will everyone be in a group of 2?
- There are 20 students in Priya’s class. Will everyone be in a group of 2?
- There are 19 students in Noah’s class. Will everyone be in a group of 2?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Draw or display:

- “How could we use this representation to show whether everyone in Noah’s class will have a partner?” (There are 18 circles and you can see they are in pairs. 19 is one more than 18. So, one circle would be left out).
- Share responses. Include reasoning from previously selected students.
Lesson Synthesis
Lesson Synthesis
Display t-chart from the last activity and the t-chart created in the previous lesson.
“What do you notice about the numbers in each chart? What do you wonder?” (I notice the numbers in the “no leftovers” group are the same on both charts. Both charts have a group that has numbers with one leftover and the numbers are the same on both charts. What other numbers go in these groups? Why are the same numbers split up in different categories on both charts? Do these numbers have a special name?)
“When the number of objects can be split into two equal groups or made into pairs without any objects left over, we say the number is even.”
“Numbers that are not even are called odd. When we try to make two equal groups of objects but there’s one left over, there is an odd number of objects. If we try to put objects into pairs but we have one left over, there is an odd number of objects.”
Add the words even and odd to each chart above the appropriate category.
Cool-down: Everybody Find a Partner (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.