Lesson 12
Applications of Arithmetic with Powers of 10
Problem 1
Which is larger: the number of meters across the Milky Way, or the number of cells in all humans? Explain or show your reasoning.
Some useful information:
- The Milky Way is about 100,000 light years across.
- There are about 37 trillion cells in a human body.
- One light year is about \(10^{16}\) meters.
- The world population is about 7 billion.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Write each number in scientific notation.
- 14,700
- 0.00083
- 760,000,000
- 0.038
- 0.38
- 3.8
- 3,800,000,000,000
- 0.0000000009
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Perform the following calculations. Express your answers in scientific notation.
-
\((2 \times 10^5) + (6 \times 10^5)\)
-
\((4.1 \times 10^7) \boldcdot 2\)
-
\((1.5 \times 10^{11}) \boldcdot 3\)
-
\((3 \times 10^3)^2\)
- \((9 \times 10^6) \boldcdot (3 \times 10^6)\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Jada is making a scale model of the solar system. The distance from Earth to the Moon is about \(2.389 \times 10^5\) miles. The distance from Earth to the Sun is about \(9.296 \times 10^7\) miles. She decides to put Earth on one corner of her dresser and the Moon on another corner, about a foot away. Where should she put the sun?
- On a windowsill in the same room?
- In her kitchen, which is down the hallway?
- A city block away?
Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Diego was solving an equation, but when he checked his answer, he saw his solution was incorrect. He knows he made a mistake, but he can’t find it. Where is Diego’s mistake and what is the solution to the equation?
\(\displaystyle \begin{align} \text-4(7-2x)=3(x+4)\\ \text-28-8x=3x+12\\ \text-28=11x+12\\ \text-40=11x\\ \text{-}\frac {40}{11}=x\ \end{align}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 13.)Problem 6
Here is the graph for one equation in a system of equations.
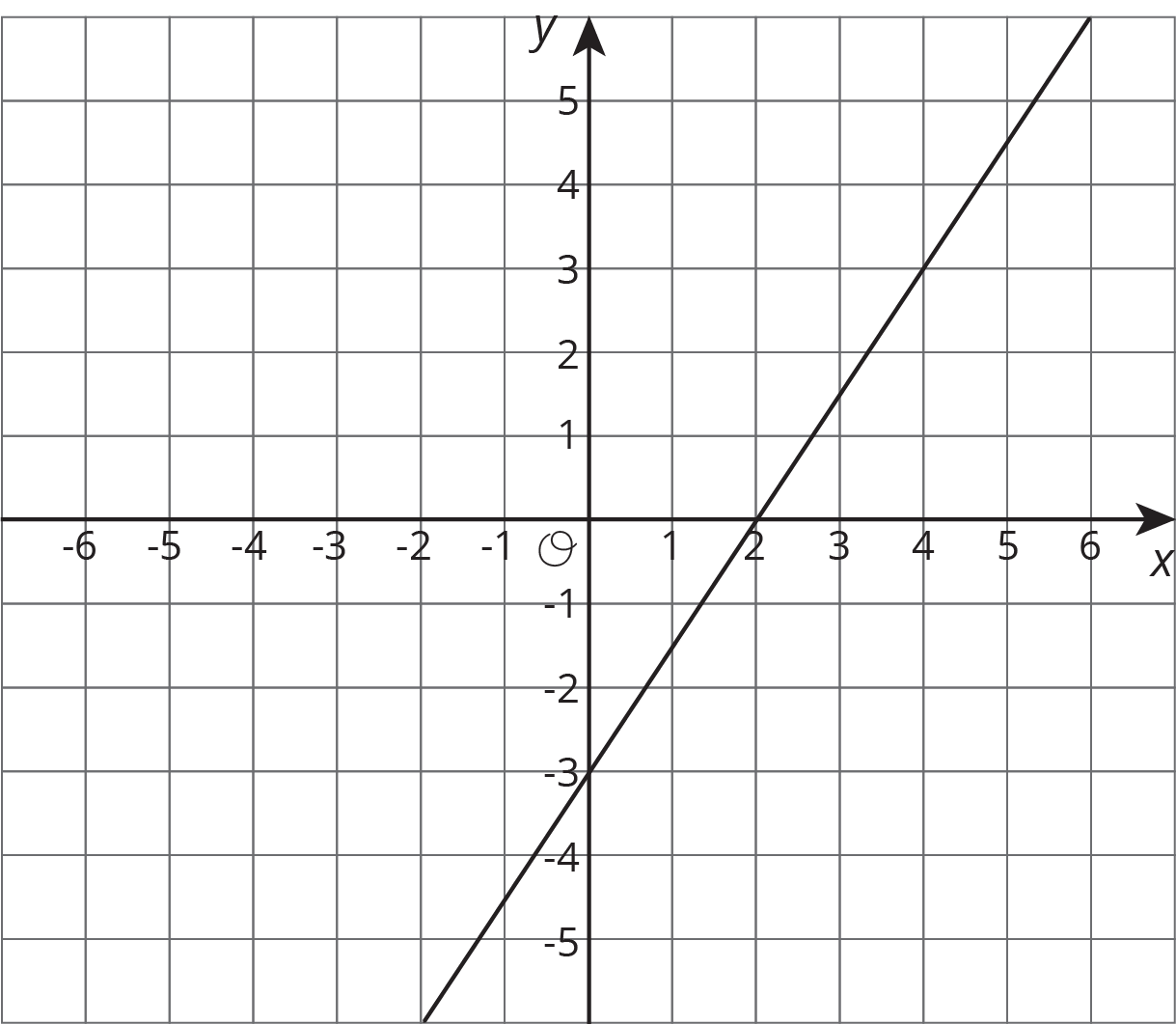
- Write a second equation for the system so it has infinitely many solutions.
- Write a second equation whose graph goes through \((0,2)\) so that the system has no solutions.
- Write a second equation whose graph goes through \((2,2)\) so that the system has one solution at \((4,3)\).
Solution
For access, consult one of our IM Certified Partners.
(From Unit 5, Lesson 13.)