Lesson 6

Distinguishing between Two Types of Situations

View Student Lesson

Problem 1

Match each equation to a story. (Two of the stories match the same equation.)

  1. \(3(x+5)=17\)
  2. \(3x+5=17\)
  3. \(5(x+3)=17\)
  4. \(5x+3=17\)
  1. Jada’s teacher fills a travel bag with 5 copies of a textbook. The weight of the bag and books is 17 pounds. The empty travel bag weighs 3 pounds. How much does each book weigh?
  2. A piece of scenery for the school play is in the shape of a 5-foot-long rectangle. The designer decides to increase the length. There will be 3 identical rectangles with a total length of 17 feet. By how much did the designer increase the length of each rectangle?
  3. Elena spends $17 and buys a $3 book and a bookmark for each of her 5 cousins. How much does each bookmark cost?
  4. Noah packs up bags at the food pantry to deliver to families. He packs 5 bags that weigh a total of 17 pounds. Each bag contains 3 pounds of groceries and a packet of papers with health-related information. How much does each packet of papers weigh?
  5. Andre has 3 times as many pencils as Noah and 5 pens. He has 17 pens and pencils all together. How many pencils does Noah have?

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Elena walked 20 minutes more than Lin. Jada walked twice as long as Elena. Jada walked for 90 minutes. The equation \(2(x+20)=90\) describes this situation. Match each expression with the statement in the story with the expression it represents.

A:

\(x\)

B:

\(x+20\)

C:

\(2(x+20)\)

D:

90

1:

The number of minutes that Jada walked

2:

The number of minutes that Elena walked

3:

The number of minutes that Lin walked

Solution

For access, consult one of our IM Certified Partners.

Problem 3

A school ordered 3 large boxes of board markers. After giving 15 markers to each of 3 teachers, there were 90 markers left. The diagram represents the situation. How many markers were originally in each box?

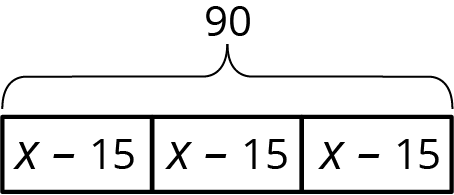
Tape diagram. Three equal parts labeled, x minus 15, total 90.

 

Solution

For access, consult one of our IM Certified Partners.

(From Unit 3, Lesson 2.)

Problem 4

Select all the pairs of points so that the line between those points has slope \(\frac 2 3\).

A:

\((0,0)\) and \((2,3)\)

B:

\((0,0)\) and \((3,2)\)

C:

\((1,5)\) and \((4,7)\)

D:

\((\text-2,\text-2)\) and \((4,2)\)

E:

\((20,30)\) and \((\text-20,\text-30)\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 16.)