Lesson 10
Dilations on a Square Grid
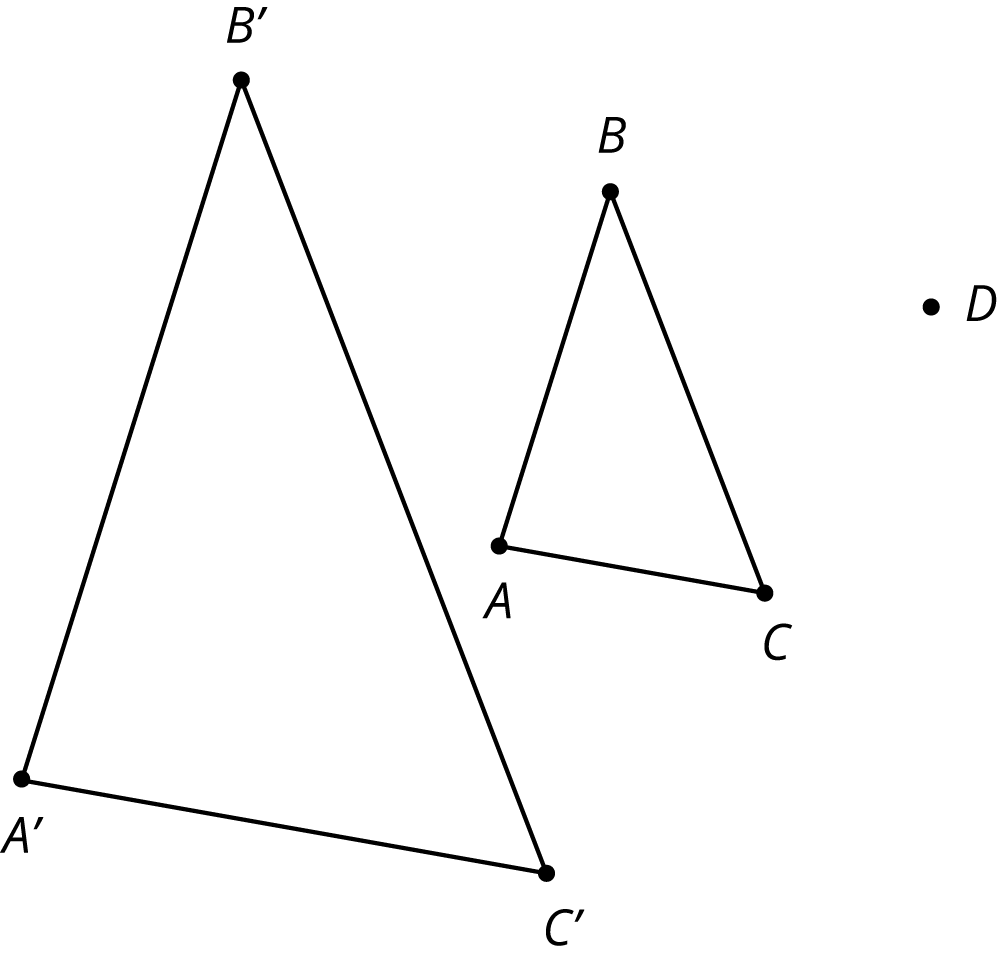
Problem 1
Triangle \(ABC\) is dilated using \(D\) as the center of dilation with scale factor 2.
The image is triangle \(A’B’C’\). Clare says the two triangles are congruent, because their angle measures are the same. Do you agree? Explain how you know.
Solution
For access, consult one of our IM Certified Partners.
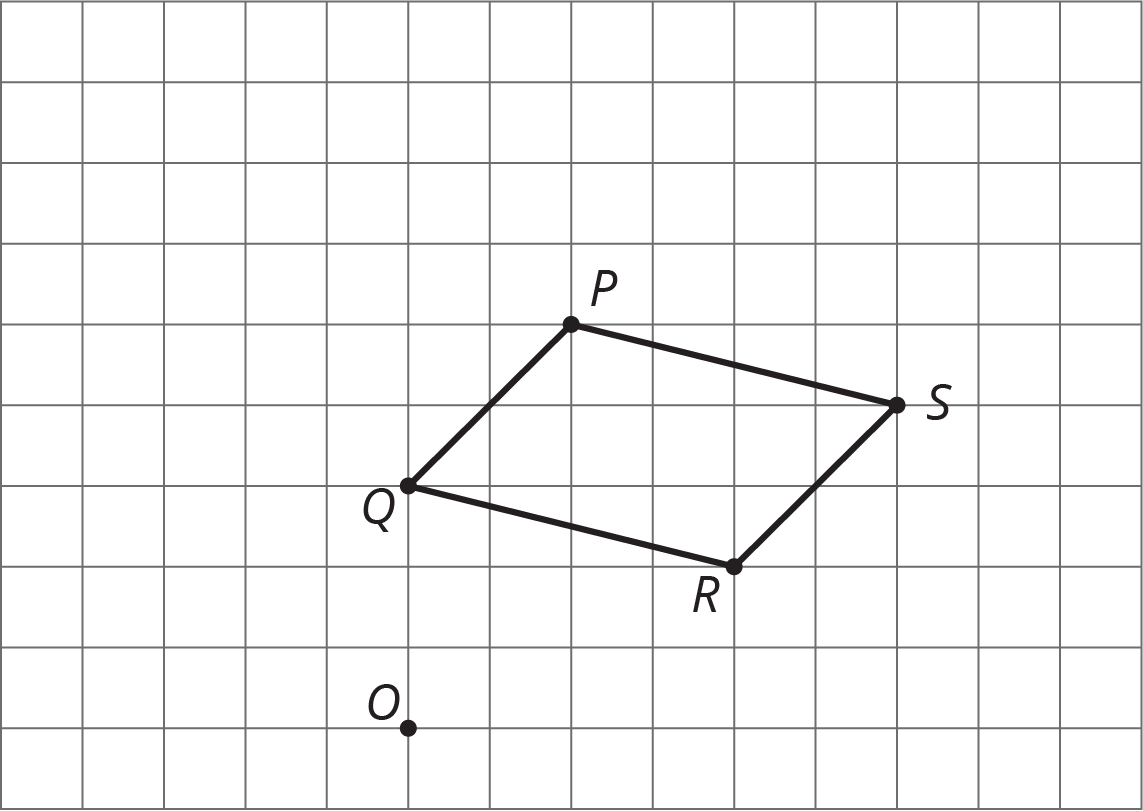
Problem 2
On graph paper, sketch the image of quadrilateral PQRS under the following dilations:
- The dilation centered at \(R\) with scale factor 2.
- The dilation centered at \(O\) with scale factor \(\frac{1}{2}\).
- The dilation centered at \(S\) with scale factor \(\frac{1}{2}\).
Solution
For access, consult one of our IM Certified Partners.
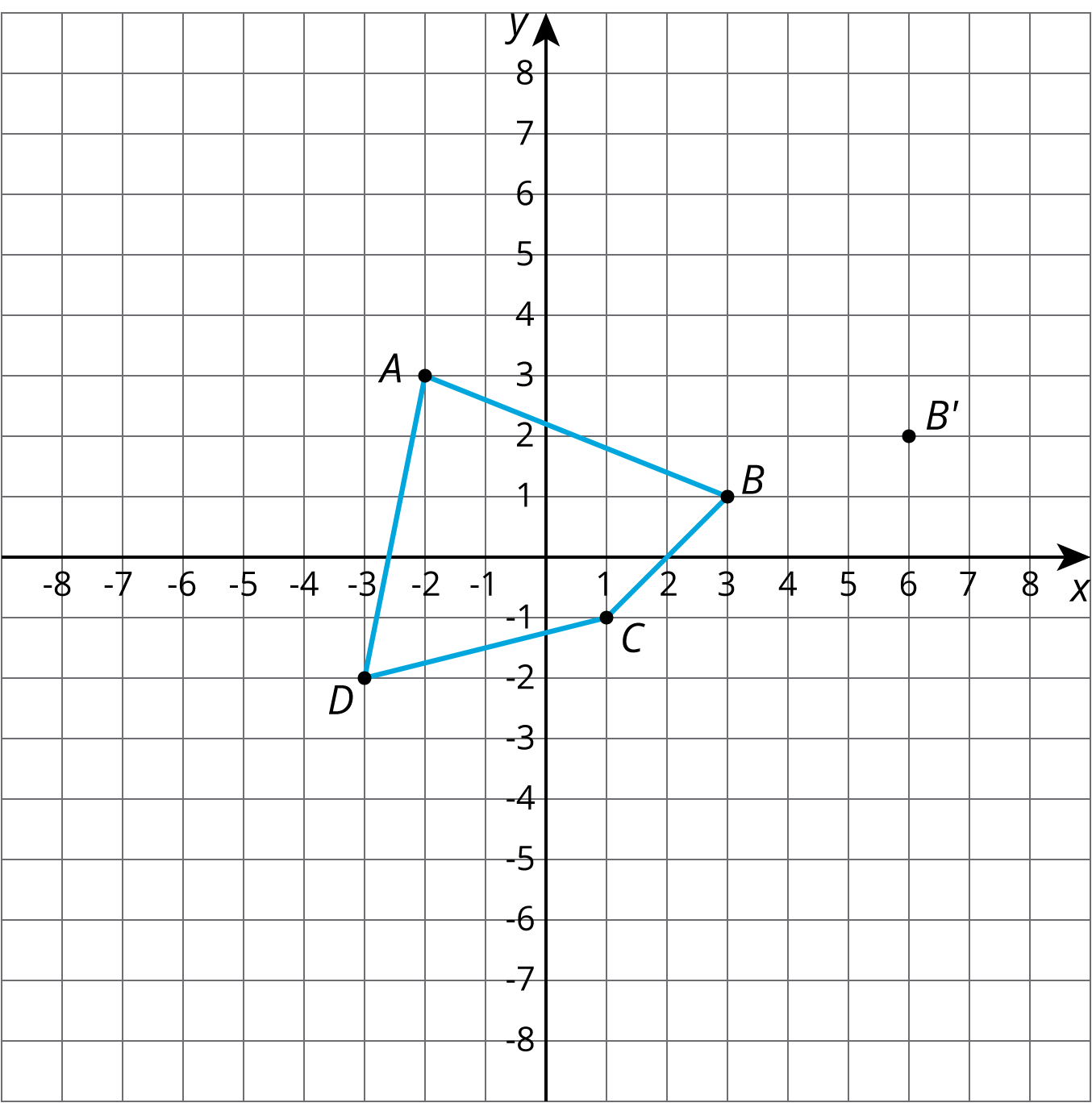
Problem 3
Quadrilateral \(ABCD\) is dilated with center \((0,0)\), taking \(B\) to \(B'\). Draw \(A'B'C'D'\).
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Triangles \(B\) and \(C\) have been built by dilating Triangle \(A\).
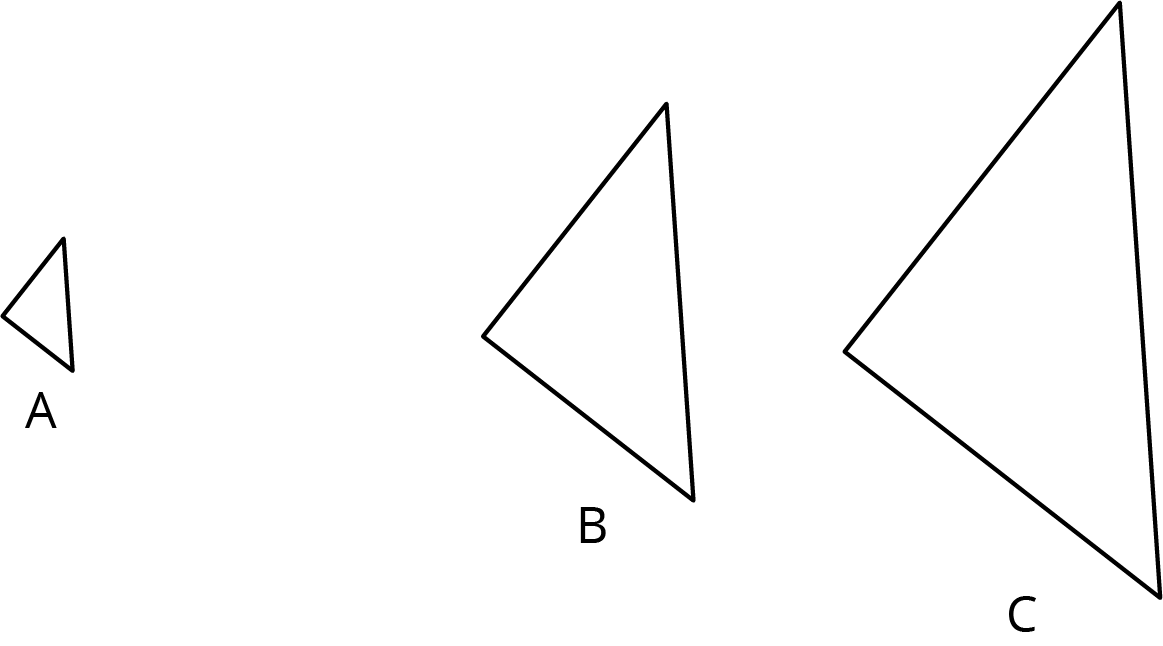
- Find the center of dilation.
- Triangle \(B\) is a dilation of \(A\) with approximately what scale factor?
- Triangle \(A\) is a dilation of \(B\) with approximately what scale factor?
- Triangle \(B\) is a dilation of \(C\) with approximately what scale factor?
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Here is a triangle.
- Draw the dilation of triangle \(ABC\), with center \((0,0)\), and scale factor 2. Label this triangle \(A’B’C’\).
- Draw the dilation of triangle \(ABC\), with center \((0,0)\), and scale factor \(\frac{1}{2}\). Label this triangle \(A’’B’’C’’\).
- Is \(A’’B’’C’’\) a dilation of triangle \(A’B’C’\)? If yes, what are the center of dilation and the scale factor?
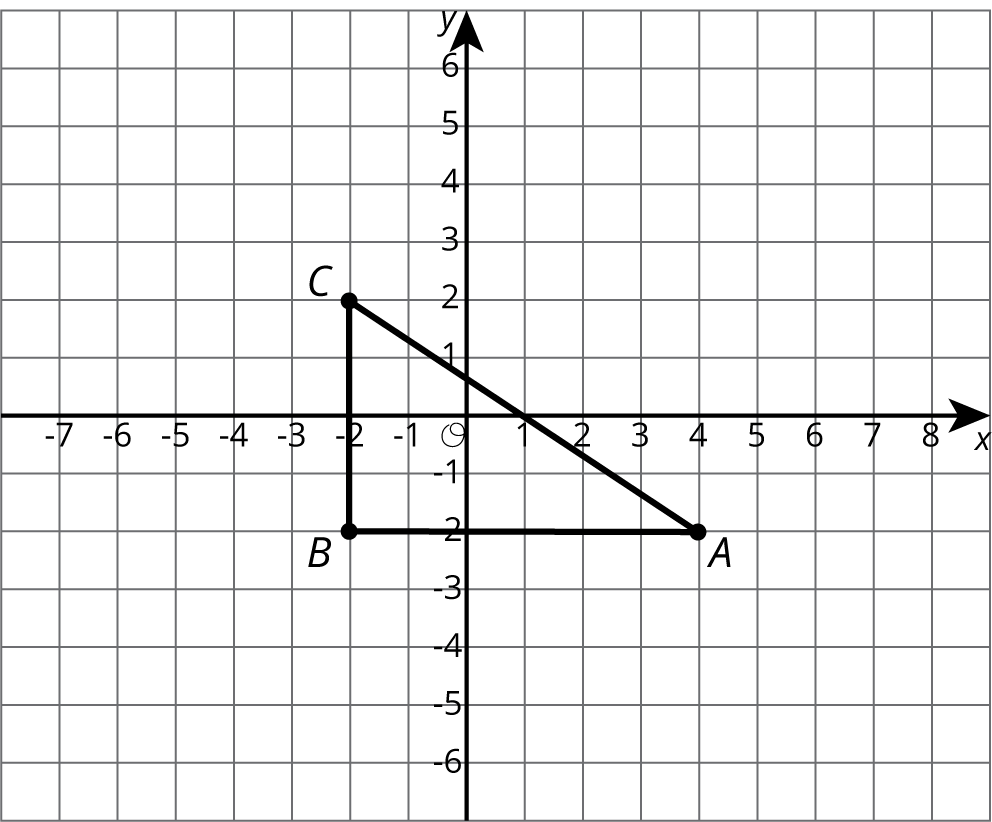
Solution
For access, consult one of our IM Certified Partners.
Problem 6
The diagram shows three lines with some marked angle measures.
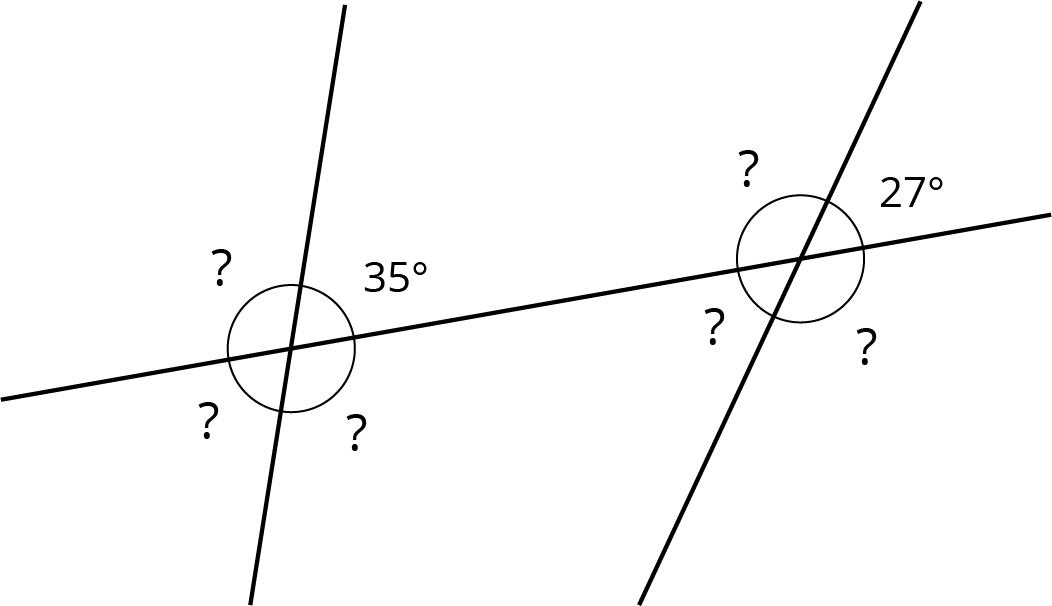
Find the missing angle measures marked with question marks.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 1, Lesson 12.)