Lesson 18
Two Related Quantities, Part 2
Problem 1
A car is traveling down a road at a constant speed of 50 miles per hour.
- Complete the table with the amounts of time it takes the car to travel certain distances, or the distances traveled for certain amounts of time.
-
Write an equation that represents the distance traveled by the car, \(d\), for an amount of time, \(t\).
- In your equation, which is the dependent variable and which is the independent variable?
| time (hours) | distance (miles) |
|---|---|
| 2 | |
| 1.5 | |
| \(t\) | |
| 50 | |
| 300 | |
| \(d\) |
Solution
For access, consult one of our IM Certified Partners.
Problem 2
The graph represents the amount of time in hours it takes a ship to travel various distances in miles.
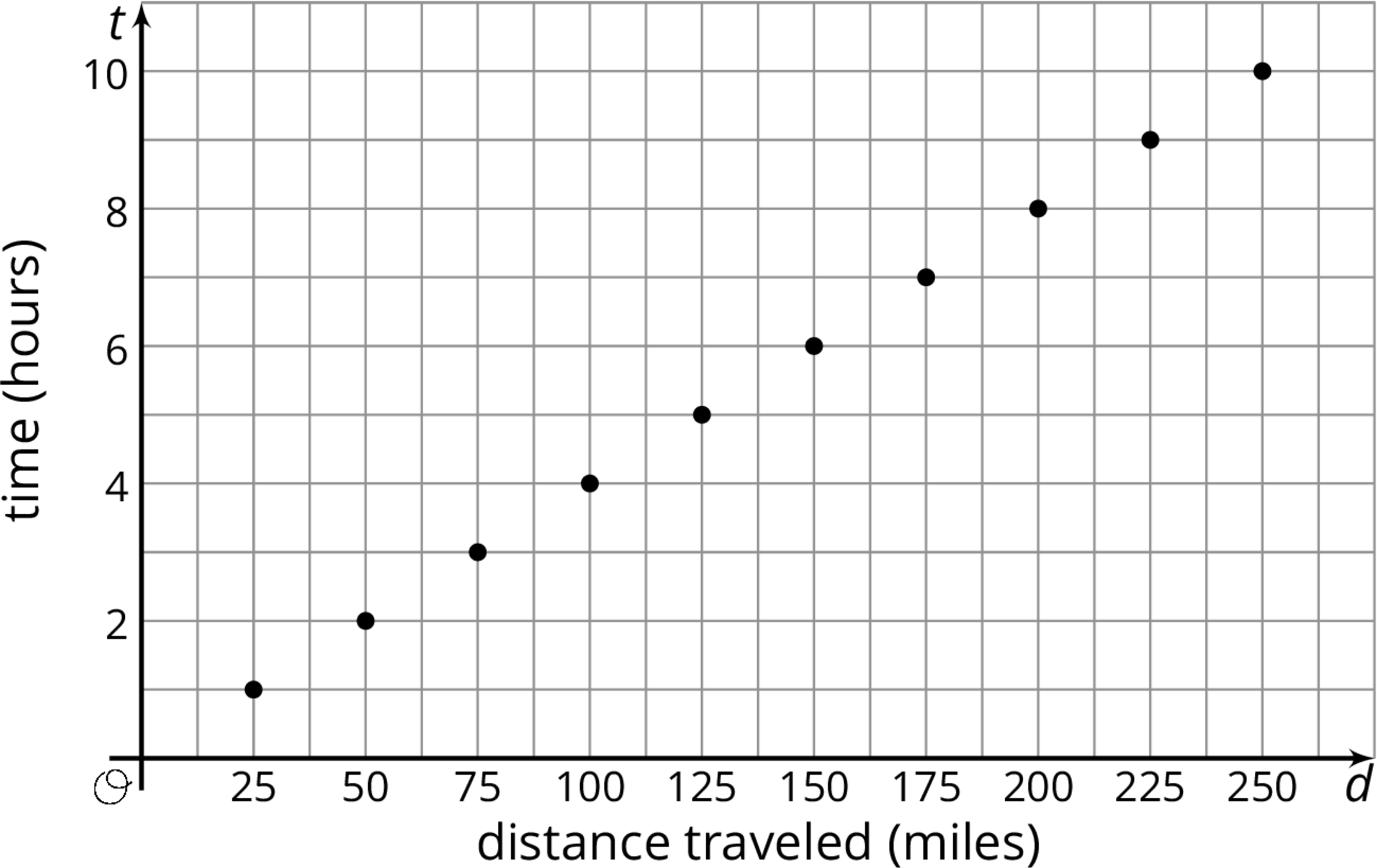
- Write the coordinates of one point on the graph. What does the point represent?
- What is the speed of the ship in miles per hour?
- Write an equation that relates the time, \(t\), it takes to travel a given distance, \(d\).
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Find a solution to each equation in the list that follows (not all numbers will be used):
-
\(2^x=8\)
-
\(2^x=2\)
-
\(x^2=100\)
-
\(x^2=\frac{1}{100}\)
-
\(x^1=7\)
-
\(2^x\boldcdot 2^3=2^7\)
-
\(\frac{2^x}{2^3}=2^5\)
List:
\(\frac{1}{10}\)
\(\frac{1}{3}\)
1
2
3
4
5
7
8
10
16
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 16.)Problem 4
Select all the expressions that are equivalent to \(5x +30x - 15x\).
\(5(x + 6x-3x)\)
\((5+30-15)\boldcdot x\)
\(x(5+30x-15x)\)
\(5x(1+6-3)\)
\(5(x+30x-15x)\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 10.)Problem 5
Evaluate each expression if \(x\) is 1, \(y\) is 2, and \(z\) is 3.
- \(7x^2-z\)
- \((x+4)^3-y\)
- \(y(x + 3^3)\)
- \((7-y+z)^2\)
- \(0.241x + x^3\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 4, Lesson 16.)