Lesson 21

In previous lessons students used double number lines to reason about percentages. Double number lines show different percentages when a given amount is identified as 100%, and emphasize that percentages are a rate per 100. In this lesson they use tape diagrams. Tape diagrams are useful for seeing the connection between percentages and fractions. For example, this tape diagram shows that 25% of a whole is the same as \(\frac14\) of that whole by showing that 25% of the whole is one part when 100% of the whole is divided into four equal parts.

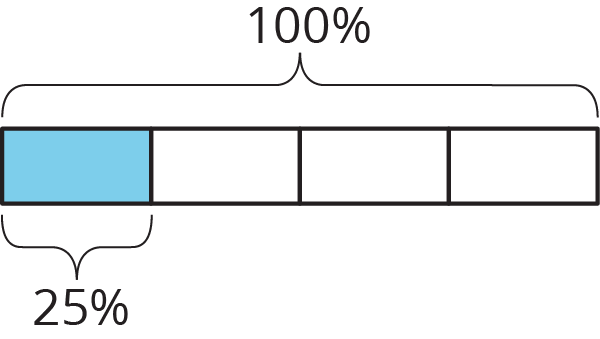
Tape diagrams are also useful in solving problems of the form \(A\) is \(B\%\) of \(C\) when you are given two of the numbers and must find the third. When reasoning about percentages, it is important to indicate the whole as 100%, just as it is important to indicate the whole when working with fractions (MP6).