Lesson 5

Areas of Parallelograms

View Student Lesson

Problem 1

Select all segments that could represent a corresponding height if the side \(m\) is the base.

A parallelogram with a bottom side labeled m and a right side labeled n. Dashed lines e, f, j, and k are drawn perpendicular to side m, and dashed lines g and h are drawn perpendicular to side n.
A:

e

B:

f

C:

g

D:

h

E:

j

F:

k

G:

n

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Find the area of each parallelogram.

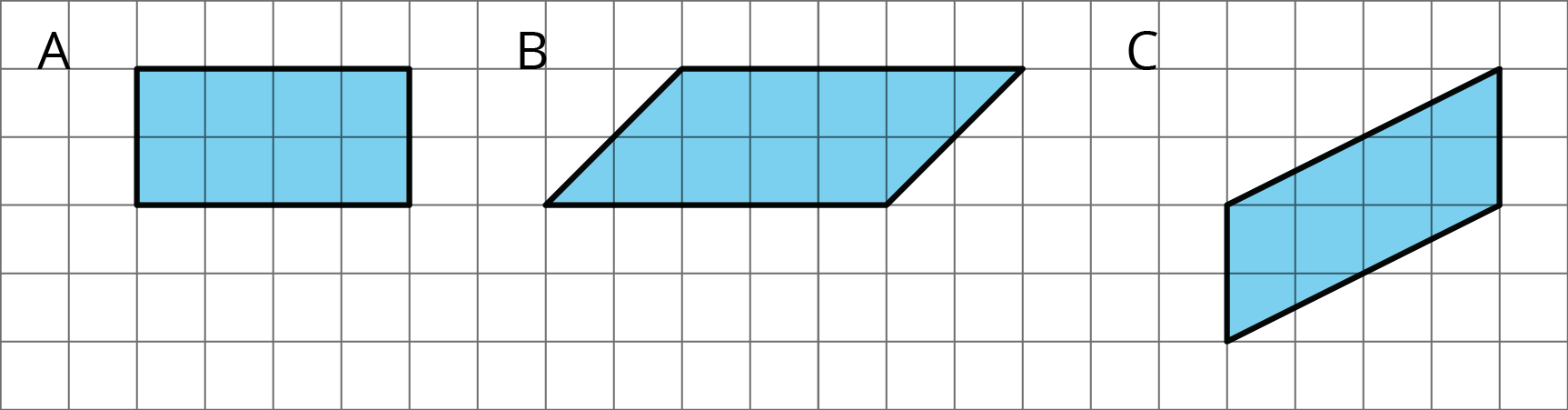
3 parallelograms on a grid, labeled A, B, C.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Find the area of each parallelogram.

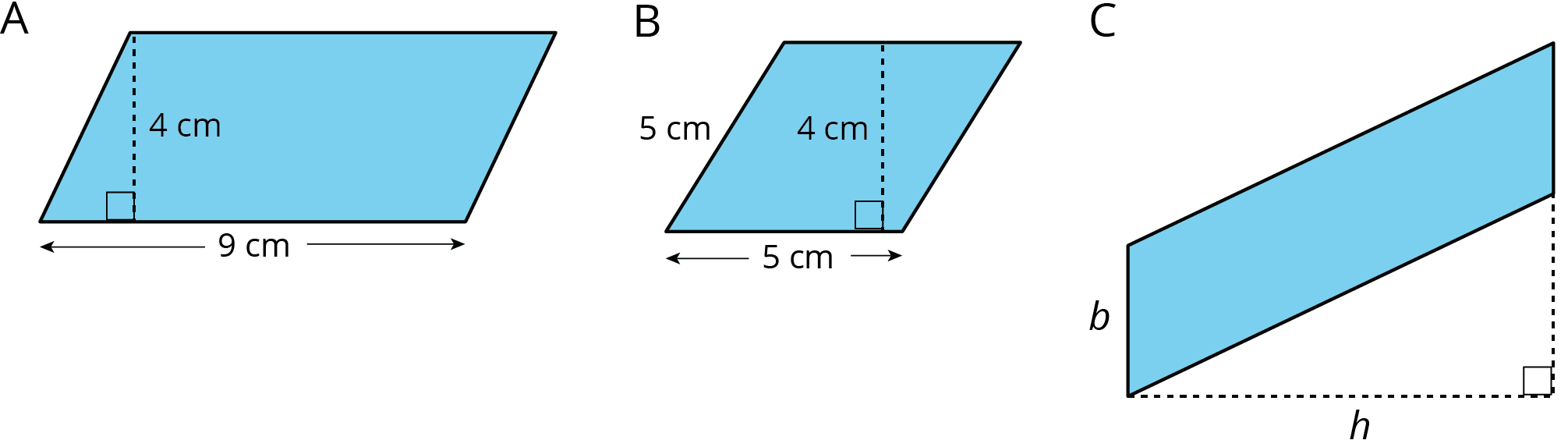
3 parallelograms labeled A, B, C. 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

The Dockland Building in Hamburg, Germany is shaped like a parallelogram.

A photograph of the Dockland Building in Hamburg, Germany. The building is shaped like a parallelogram.

If the length of the building is 86 meters and its height is 55 meters, what is the area of this face of the building?

 

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Do you agree with each of these statements? Explain your reasoning.

  1. A parallelogram has six sides.
  2. Opposite sides of a parallelogram are parallel.
  3. A parallelogram can have one pair or two pairs of parallel sides. 
  4. All sides of a parallelogram have the same length.
  5. All angles of a parallelogram have the same measure. 

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 4.)

Problem 6

A square with an area of 1 square meter is decomposed into 9 identical small squares. Each small square is decomposed into two identical triangles.

  1. What is the area, in square meters, of 6 triangles? If you get stuck, consider drawing a diagram.
  2. How many triangles are needed to compose a region that is \(1\frac 12\) square meters?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 2.)

Problem 7

Find the area of the shaded region. All measurements are in centimeters. Show your reasoning.

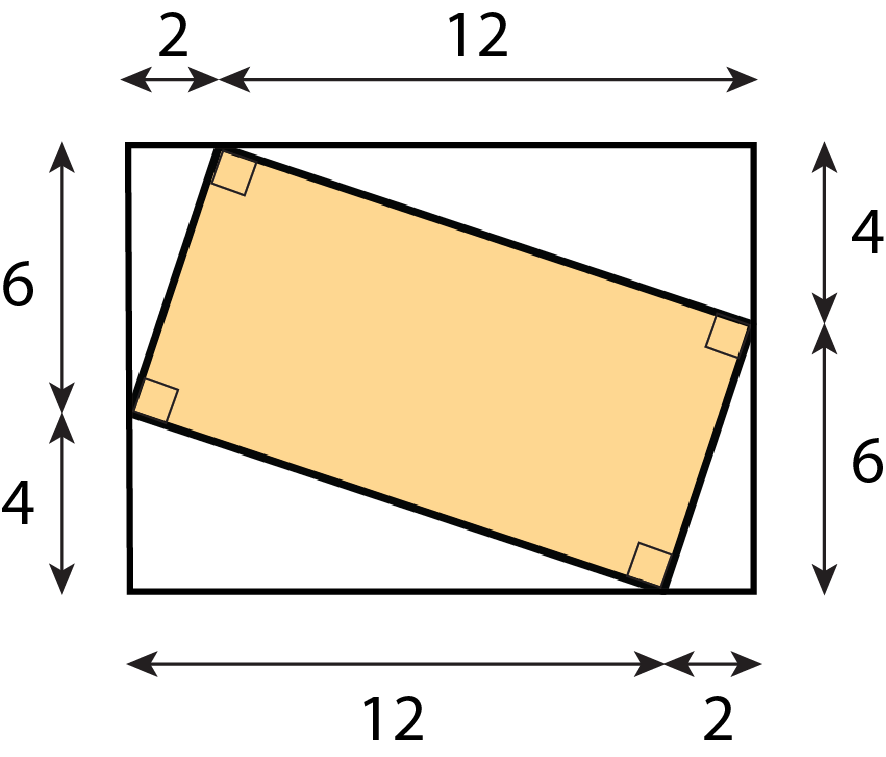
A shaded rectangle located at an angle within a larger rectangle. 

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 3.)