Lesson 9
Combining Like Terms (Part 1)
Let's see how we can tell that expressions are equivalent.
Problem 1
Andre says that \(10x+6\) and \(5x+11\) are equivalent because they both equal 16 when \(x\) is 1. Do you agree with Andre? Explain your reasoning.
Problem 2
Select all expressions that can be subtracted from \(9x\) to result in the expression \(3x+5\).
\(\text-5+6x\)
\(5-6x\)
\(6x+5\)
\(6x-5\)
\(\text-6x+5\)
Problem 3
Select all the statements that are true for any value of \(x\).
\(7x + (2x+7) = 9x+7\)
\(7x + (2x - 1) = 9x + 1\)
\(\frac12 x+(3 - \frac12 x)=3\)
\(5x - (8 - 6x) =\text-x-8\)
\(0.4x - (0.2x+8) =0.2x-8\)
\(6x - (2x -4)=4x+4\)
Problem 4
For each situation, would you describe it with \(x< 25\), \(x > 25\), \(x \leq 25\), or \(x \geq 25\)?
- The library is having a party for any student who read at least 25 books over the summer. Priya read \(x\) books and was invited to the party.
- Kiran read \(x\) books over the summer but was not invited to the party.
-

-

Problem 5
A line is represented by the equation \(\frac{y}{x-2}=\frac{3}{11}\). What are the coordinates of some points that lie on the line? Graph the line on graph paper.
Problem 6
Select all the statements that must be true for any scaled copy Q of Polygon P.
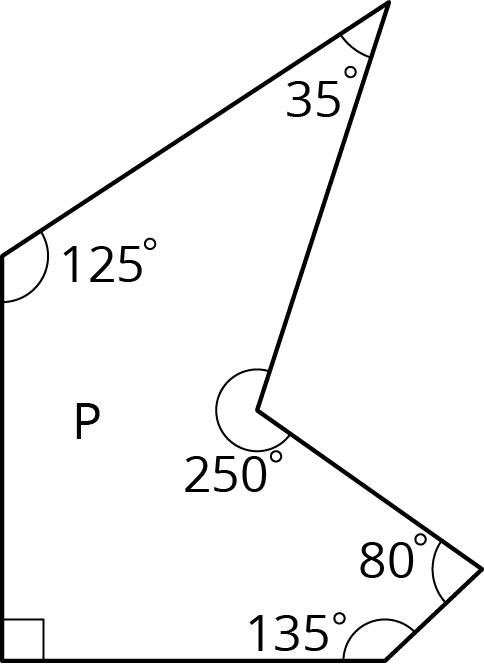
The side lengths are all whole numbers.
The angle measures are all whole numbers.
Q has exactly 1 right angle.
If the scale factor between P and Q is \(\frac15\), then each side length of P is multiplied by \(\frac15\) to get the corresponding side length of Q.
If the scale factor is 2, each angle in P is multiplied by 2 to get the corresponding angle in Q.
Q has 2 acute angles and 3 obtuse angles.