Lesson 11

1. Choose a horizontal or a vertical line on the grid. Draw 4 points on the line and label each point with its coordinates.

   

   

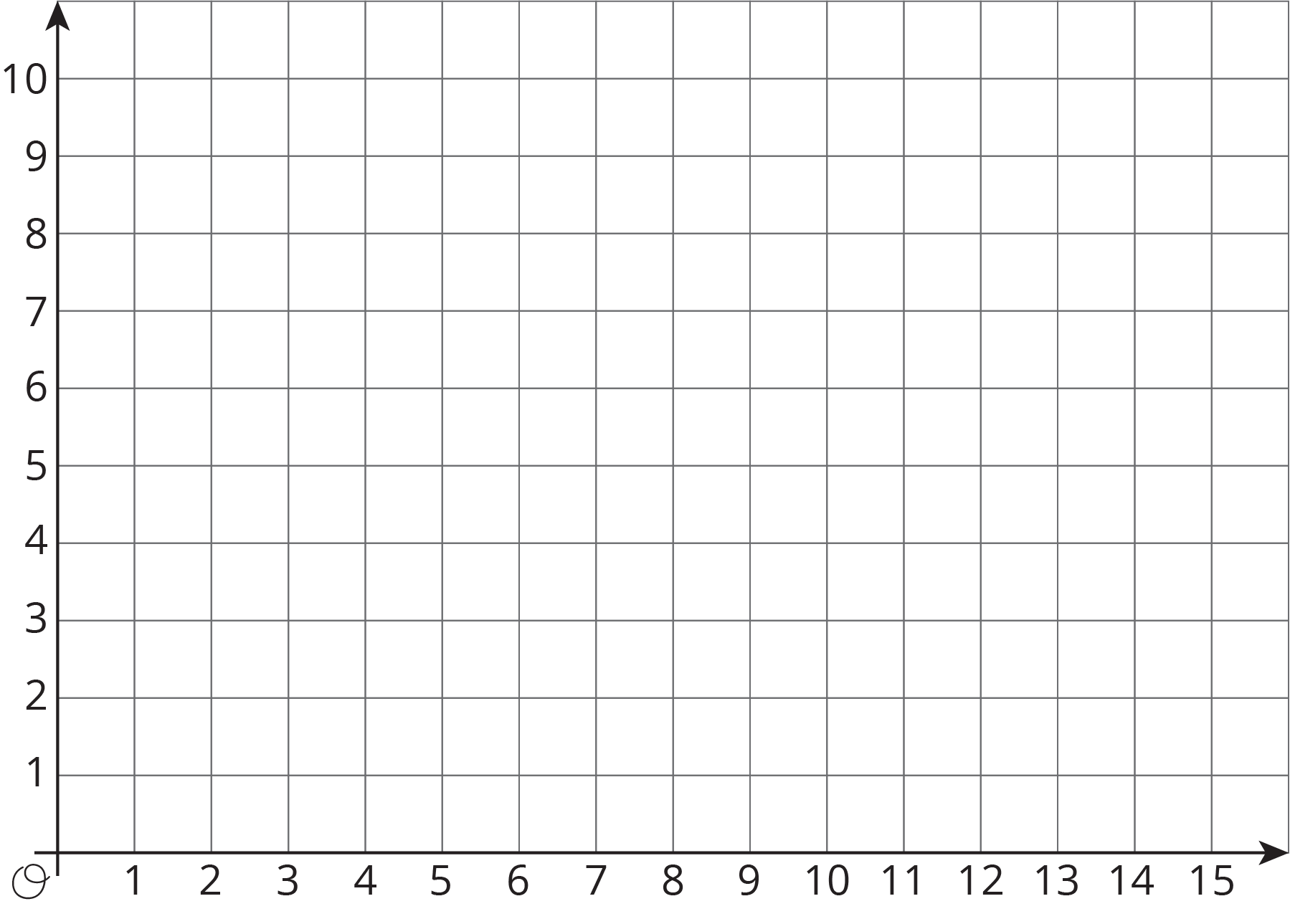
2. Tell your partner whether your line is horizontal or vertical, and have your partner guess the locations of your points by naming coordinates.

   If a guess is correct, put an X through the point. If your partner guessed a point that is on your line but not the point that you plotted, say, “That point is on my line, but is not one of my points.”

   Take turns guessing each other’s points, 3 guesses per turn.

1. 

   

   The colored points on the coordinate plane are like targets. Hit each point by entering its coordinates as an ordered pair in the Input Bar, like this:
2. What do you notice about the locations and ordered pairs of \(B\), \(C\), and \(D\)? How are they different from those for point \(A\)?

3. Plot a point at \((\text-2, 5)\). Label it \(E\). Plot another point at \((3, \text-4.5)\). Label it \(F\).

4. The coordinate plane is divided into four quadrants, I, II, III, and IV, as shown here.

   

   

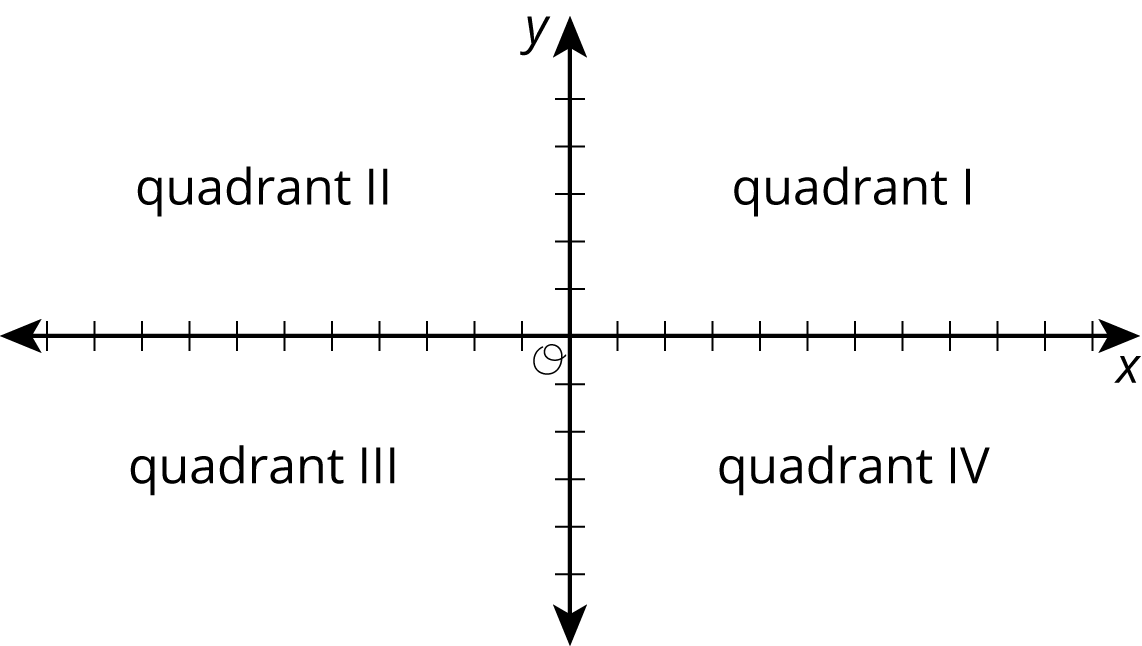
   • \(G = (5, 2)\)
   • \(H=(\text-1, \text-5)\)
   • \(I=(7,\text-4)\)
   1. In which quadrant is \(G\) located? \(H\)? \(I\)?
   2. A point has a positive \(y\)-coordinate. In which quadrant could it be?

1. Here are three sets of coordinates. For each set, draw and label an appropriate pair of axes and plot the points.

   1. \((1, 2), (3, \text-4), (\text-5, \text-2), (0, 2.5)\)

      

      

   2. \((50, 50), (0, 0), (\text-10, \text-30), (\text-35, 40)\)

      

      

   3. \(\left(\frac14, \frac34\right), \left(\frac {\text{-}5}{4}, \frac12\right), \left(\text-1\frac14, \frac {\text{-}3}{4}\right), \left(\frac14, \frac {\text{-}1}{2}\right)\)

      

      

2. Discuss with a partner:

   • How are the axes and labels of your three drawings different?
   • How did the coordinates affect the way you drew the axes and label the numbers?

Just as the number line can be extended to the left to include negative numbers, the \(x\)- and \(y\)-axis of a coordinate plane can also be extended to include negative values.

The ordered pair \((x,y)\) can have negative \(x\)- and \(y\)-values. For \(B= (\text-4,1)\), the \(x\)-value of -4 tells us that the point is 4 units to the left of the \(y\)-axis. The \(y\)-value of 1 tells us that the point is one unit above the \(x\)-axis.

The same reasoning applies to the points \(A\) and \(C\). The \(x\)- and \(y\)-coordinates for point \(A\) are positive, so \(A\) is to the right of the \(y\)-axis and above the \(x\)-axis. The \(x\)- and \(y\)-coordinates for point \(C\) are negative, so \(C\) is to the left of the \(y\)-axis and below the \(x\)-axis.