Lesson 11
Error Intervals
Let’s solve more problems about percent error.
11.1: A Lot of Iron Ore
An industrial scale is guaranteed by the manufacturer to have a percent error of no more than 1%. What is a possible reading on the scale if you put 500 kilograms of iron ore on it?
11.2: Saw Mill
-
A saw mill cuts boards that are 16 ft long. After they are cut, the boards are inspected and rejected if the length has a percent error of 1.5% or more.
- List some board lengths that should be accepted.
- List some board lengths that should be rejected.
- The saw mill also cuts boards that are 10, 12, and 14 feet long. An inspector rejects a board that was 2.3 inches too long. What was the intended length of the board?
11.3: Info Gap: Quality Control
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Summary
Percent error is often used to express a range of possible values. For example, if a box of cereal is guaranteed to have 750 grams of cereal, with a margin of error of less than 5%, what are possible values for the actual number of grams of cereal in the box? The error could be as large as \((0.05) \boldcdot 750 = 37.5\) and could be either above or below than the correct amount.
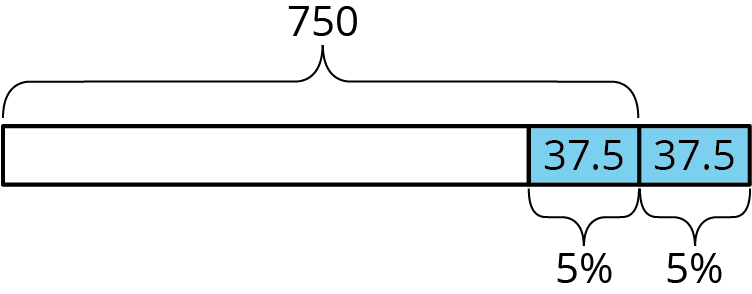
Therefore, the box can have anywhere between 712.5 and 787.5 grams of cereal in it, but it should not have 700 grams or 800 grams, because both of those are more than 37.5 grams away from 750 grams.
Glossary Entries
- measurement error
Measurement error is the positive difference between a measured amount and the actual amount.
For example, Diego measures a line segment and gets 5.3 cm. The actual length of the segment is really 5.32 cm. The measurement error is 0.02 cm, because \(5.32-5.3=0.02\).
- percent error
Percent error is a way to describe error, expressed as a percentage of the actual amount.
For example, a box is supposed to have 150 folders in it. Clare counts only 147 folders in the box. This is an error of 3 folders. The percent error is 2%, because 3 is 2% of 150.