What Students Should Know and Be Able to Do

Our ultimate purpose is to impact student learning and achievement. First, we define the attitudes and beliefs about mathematics and mathematics learning we want to cultivate in students, and what mathematics students should know and be able to do.

Attitudes and Beliefs We Want to Cultivate

Many people think that mathematical knowledge and skills exclusively belong to “math people.” Yet research shows that students who believe that hard work is more important than innate talent learn more mathematics.¹ We want students to believe anyone can do mathematics and that persevering at mathematics will result in understanding and success. In the words of the NRC report Adding It Up, we want students to develop a “productive disposition—[the] habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.”²

¹ Uttal, D.H. (1997). Beliefs about genetic influences on mathematics achievement: a cross-cultural comparison. Genetica, 99(2-3), 165-172. doi.org/10.1023/A:1018318822120

² National Research Council. (2001). Adding it up: Helping children learn mathematics. J.Kilpatrick, J. Swafford, and B.Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press. doi.org/10.17226/9822

Knowledge

Conceptual understanding: Students need to understand the why behind the how in mathematics. Concepts build on experience with concrete contexts. Students should access these concepts from a number of perspectives in order to see math as more than a set of disconnected procedures.

Procedural fluency: We view procedural fluency as solving problems expected by the standards with speed, accuracy, and flexibility.

Application: Application means applying mathematical or statistical concepts and skills to a novel mathematical or real-world context.

These three aspects of mathematical proficiency are interconnected: procedural fluency is supported by understanding, and deep understanding often requires procedural fluency. In order to be successful in applying mathematics, students must both understand and be able to do the mathematics.

Mathematical Practices

In a mathematics class, students should not just learn about mathematics, they should do mathematics. This can be defined as engaging in the mathematical practices: making sense of problems, reasoning abstractly and quantitatively, making arguments and critiquing the reasoning of others, modeling with mathematics, making appropriate use of tools, attending to precision in their use of language, looking for and making use of structure, and expressing regularity in repeated reasoning.

What Teaching and Learning Should Look Like

How teachers should teach depends on what we want students to learn. To understand what teachers need to know and be able to do, we need to understand how students develop the different (but intertwined) strands of mathematical proficiency, and what kind of instructional moves support that development.

Principles for Mathematics Teaching and Learning

Active learning is best: Students learn best and retain what they learn better by solving problems. Often, mathematics instruction is shaped by the belief that if teachers tell students how to solve problems and then students practice, students will learn how to do mathematics.

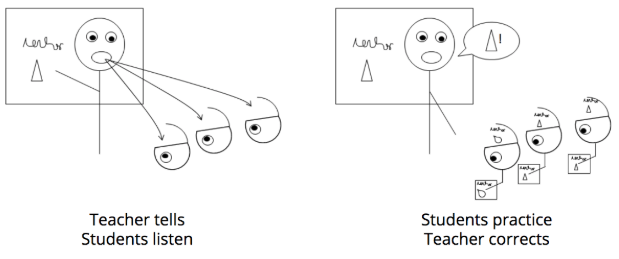
Decades of research tells us that the traditional model of instruction is flawed. Traditional instructional methods may get short-term results with procedural skills, but students tend to forget the procedural skills and do not develop problem solving skills, deep conceptual understanding, or a mental framework for how ideas fit together. They also don’t develop strategies for tackling non-routine problems, including a propensity for engaging in productive struggle to make sense of problems and persevere in solving them.

In order to learn mathematics, students should spend time in math class doing mathematics.

“Students learn mathematics as a result of solving problems. Mathematical ideas are the outcomes of the problem-solving experience rather than the elements that must be taught before problem solving.”³

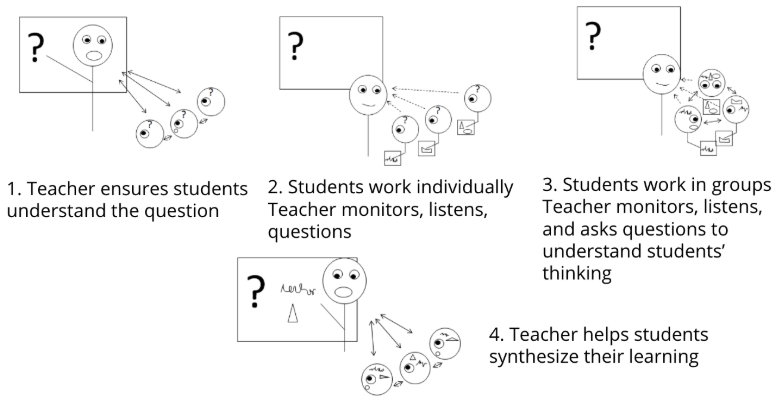
Students should take an active role, both individually and in groups, to see what they can figure out before having things explained to them or being told what to do. Teachers play a critical role in mediating student learning, but that role looks different than simply showing, telling, and correcting. The teacher’s role is

1. to ensure students understand the context and what is being asked
2. ask questions to advance students’ thinking in productive ways
3. help students share their work and understand others’ work through orchestrating productive discussions
4. synthesize the learning with students at the end of activities and lessons

Teachers should build on what students know: New mathematical ideas are built on what students already know about mathematics and the world, and as they learn new ideas, students need to make connections between them.⁴ In order to do this, teachers need to understand what knowledge students bring to the classroom and monitor what they do and do not understand as they are learning. Teachers must themselves know how the mathematical ideas connect in order to mediate students’ learning.

Good instruction starts with explicit learning goals: Learning goals must be clear not only to teachers, but also to students, and they must influence the activities in which students participate. Without a clear understanding of what students should be learning, activities in the classroom, implemented haphazardly, have little impact on advancing students’ understanding. Strategic negotiation of whole-class discussion on the part of the teacher during an activity synthesis is crucial to making the intended learning goals explicit. Teachers need to have a clear idea of the destination for the day, week, month, and year, and select and sequence instructional activities (or use well-sequenced materials) that will get the class to their destinations. If you are going to a party, you need to know the address and also plan a route to get there; driving around aimlessly will not get you where you need to go.

Different learning goals require different instructional moves: The kind of instruction that is appropriate at any given time depends on the learning goals of a particular lesson. Lessons and activities can:

• Introduce students to a new topic of study and invite them to the mathematics.
• Study new concepts and procedures deeply.
• Integrate and connect representations, concepts, and procedures.
• Work towards mastery.
• Apply mathematics.

Lessons should be designed based on what the intended learning outcomes are. This means that teachers should have a toolbox of instructional moves that they can use as appropriate.

Each and every student should have access to the mathematical work: With proper structures, accommodations, and supports, all students can learn mathematics. Teachers’ instructional toolboxes should include knowledge of and skill in implementing supports for different learners.

³ Hiebert, J., et. al. (1996). Problem solving as a basis for reform in curriculum and instruction: the case of mathematics. Educational Researcher 25(4), 12-21. doi.org/10.3102/0013189X025004012

⁴ National Research Council. (2001). Adding it up: Helping children learn mathematics. J.Kilpatrick, J. Swafford, and B.Findell (Eds.). Mathematics Learning Study Committee, Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press. doi.org/10.17226/9822

Critical Practices

Intentional planning: Because different learning goals require different instructional moves, teachers need to be able to plan their instruction appropriately. While a high-quality curriculum does reduce the burden for teachers to create or curate lessons and tasks, it does not reduce the need to spend deliberate time planning lessons and tasks. Instead, teachers’ planning time can shift to high-leverage practices (practices that teachers without a high-quality curriculum often report wishing they had more time for): reading and understanding the high-quality curriculum materials; identifying connections to prior and upcoming work; diagnosing students' readiness to do the work; leveraging instructional routines to address different student needs and differentiate instruction; anticipating student responses that will be important to move the learning forward; planning questions and prompts that will help students attend to, make sense of, and learn from each other's work; planning supports and extensions to give as many students as possible access to the main mathematical goals; figuring out timing, pacing, and opportunities for practice; preparing necessary supplies; and the never-ending task of giving feedback on student work.

Establishing norms: Norms around doing math together and sharing understandings play an important role in the success of a problem-based curriculum. For example, students must feel safe taking risks, listen to each other, disagree respectfully, and honor equal air time when working together in groups. Establishing norms helps teachers cultivate a community of learners where making thinking visible is both expected and valued.

Building a shared understanding of a small set of instructional routines: Instructional routines allow the students and teacher to become familiar with the classroom choreography and what they are expected to do. This means that they can pay less attention to what they are supposed to do and more attention to the mathematics to be learned. Routines can provide a structure that helps strengthen students’ skills in communicating their mathematical ideas.

Using high quality curriculum: A growing body of evidence suggests that using a high-quality, coherent curriculum can have a significant impact on student learning.⁵ Creating a coherent, effective instructional sequence from the ground up takes significant time, effort, and expertise. Teaching is already a full-time job, and adding curriculum development on top of that means teachers are overloaded or shortchanging their students.

Ongoing formative assessment: Teachers should know what mathematics their students come into the classroom already understanding, and use that information to plan their lessons. As students work on problems, teachers should ask questions to better understand students’ thinking, and use expected student responses and potential misconceptions to build on students’ mathematical understanding during the lesson. Teachers should monitor what their students have learned at the end of the lesson and use this information to provide feedback and plan further instruction.

⁵ Steiner, D. (2017). Curriculum research: What we know and where we need to go. Standards Work. Retrieved from https://standardswork.org/wp-content/uploads/2017/03/sw-curriculum-research-report-fnl.pdf