Lesson 6
Writing Equations for Exponential Functions
6.1: All Equivalent? (5 minutes)
Warm-up
Most fractional exponents students have encountered so far in the unit are unit fractions. This warm-up allows students to recall how to interpret exponents that are non-unit fractions. Students are given a set of expressions that are all equivalent and asked to explain why they are so. In doing so, they practice applying properties of exponents and recall how to make sense of an expression such as \(8 ^{\frac23}\).
Student Facing
- Discuss with a partner why the following expressions are equivalent.
- \(64^\frac13\)
- \(\left(8^2\right)^\frac13\)
- \(\left(2^3\right)^\frac23\)
- \(\left(8^\frac13 \right)^2\)
- \(8^\frac23\)
- What is another expression equivalent to these?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share their explanations as to why each expression is equivalent to the others. Time permitting, after a student shares their reasoning for a particular expression, ask if others thought about the same expression differently.
If not mentioned in students’ explanations, highlight that each of the expressions can be shown to be equivalent to \(8^\frac23\). Also point out that all expressions are equivalent because when each is raised to the third power, it is equal to \(8^2\).
6.2: Info Gap: Two Points (25 minutes)
Activity
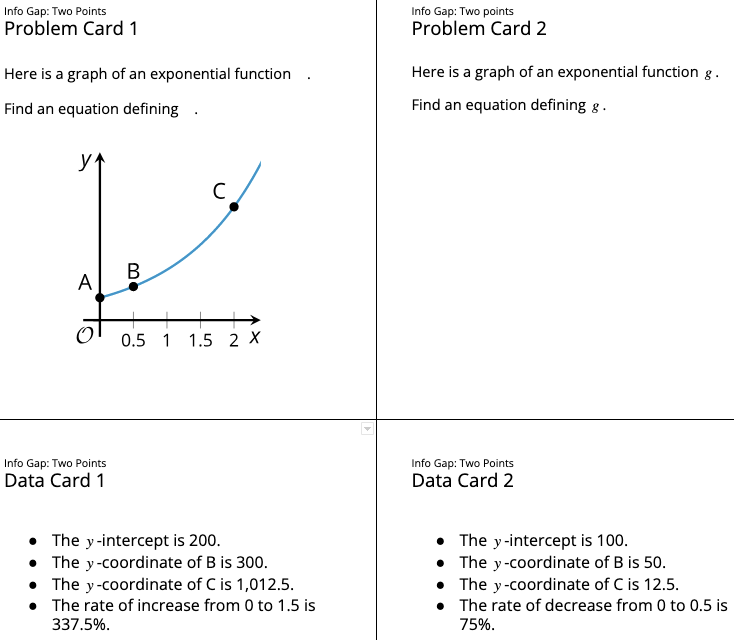
This Info Gap activity gives students an opportunity to apply their understanding that exponential functions change by equal factors over equal intervals to solve problems. In the previous lesson, students found an exponential function given two points on the graph. The work here is similar but there is no context, and the Info Gap structure requires students to think carefully about what information they can use to write the function. As in the previous task, the key is to recognize that they need the growth factor for a unit interval and the \(y\)-intercept in order to determine the function. Three points are labeled on each graph, providing students an opportunity to think strategically about which coordinates would be most effective for determining the \(y\)-intercept and the growth rate when the input increases by 1.
The Info Gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
Here is the text of the cards for reference and planning:
Launch
Tell students they will continue to determine equations for exponential functions. Explain the info gap structure, and consider demonstrating the protocol if students are unfamiliar with it.
Arrange students in groups of 2. In each group, distribute a problem card to one student and a data card to the other student. After reviewing their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Design Principle(s): Cultivate Conversation
Supports accessibility for: Memory; Organization
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the data card:
- Silently read the information on your card.
- Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
- Before telling your partner the information, ask “Why do you need to know (that piece of information)?”
- Read the problem card, and solve the problem independently.
- Share the data card, and discuss your reasoning.
If your teacher gives you the problem card:
- Silently read your card and think about what information you need to answer the question.
- Ask your partner for the specific information that you need.
- Explain to your partner how you are using the information to solve the problem.
- When you have enough information, share the problem card with your partner, and solve the problem independently.
-
Read the data card, and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Here is a graph representing a function of the form \(h(x) = ab^x\).

Find the values of \(a\) and \(b\). Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may try to find the growth factors by guessing and checking. Encourage them to think about how an exponential function changes over equal intervals (for example, how does the output change every time the input increases by 1 or by \(\frac12\)?) and use that information to find the growth factor of a function.
Activity Synthesis
After students have completed their work, share the correct answers and ask students to discuss the process of solving the problems. Ask, “What information do you need to write an exponential function?” (The starting value or \(y\)-intercept and the growth factor when \(x\) increases by 1, the '\(a\)' and '\(b\)' in \(ab^x\).)
Also highlight different methods students used to find the growth factor when the input increases by 1.
- using the \(y\)-intercept and the \(y\)-coordinate of \(B\)
- using the \(y\)-intercept and the \(y\)-coordinate of \(C\)
- using the \(y\)-coordinates of \(B\) and \(C\)
In all cases, more work is needed because the \(x\)-coordinates of the given points do not differ by 1. In particular, for Problem Card 1, if students ask for the \(y\)-coordinate of \(B\), this can be used to get the growth factor for an input increase of \(\frac{1}{2}\) and then this can be squared to get the growth factor for an input increase of 1. If students ask for the \(y\)-coordinate of \(C\), then this can be used to calculate the growth factor for an input increase of 2 and then the square root of this is the growth factor for an input increase of 1.
6.3: Bacteria Growth Expressions (10 minutes)
Optional activity
This optional activity looks at two different but equivalent expressions for an exponential growth situation. One of the expressions highlights the fact the bacteria doubles every 10 hours, while the other expression highlights the hourly growth factor given by the expression \(2^{\frac{1}{10}}\). It is important to be able to work fluently between expressions in order to choose one which best communicates a quantity of interest. For exponential expressions, there are always many choices, and for those studied here, the link between them is the property of exponents that \(\left(x^a\right)^b = x^{ab}\).
Launch
Design Principle(s): Optimize output (for justification); Cultivate conversation
Supports accessibility for: Language; Conceptual processing
Student Facing
A bacteria population starts at 1000 and doubles every 10 hours.
- Explain why the expressions \(1000 \boldcdot \left(2^{\frac{1}{10}}\right)^h\) and \(1000 \boldcdot 2^{\frac{h}{10}}\) both represent the bacteria population after \(h\) hours.
- By what factor does the bacteria population grow each hour? Explain how you know.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Highlight that the expression \(1,\!000 \boldcdot \left(2^{\frac{1}{10}}\right)^h\) shows the hourly growth rate readily. Increasing \(h\) by 1 gives \(1,\!000 \boldcdot \left(2^{\frac{1}{10}}\right)^{h+1}\) and this is equivalent to \(\left(2^{\frac{1}{10}}\right) \boldcdot \left(2^{\frac{1}{10}}\right)^h\). This means that the hourly growth factor is \(2^{\frac{1}{10}}\).
If some students used the second expression to show the hourly growth rate, invite them to share. Increasing \(h\) by 1 gives \(1,\!000 \boldcdot 2^{\frac{h+1}{10}}\) which is equivalent to \(1,\!000 \boldcdot 2^{\frac{h}{10}} \boldcdot \left(2^{\frac{1}{10}}\right)\), again showing an hourly growth factor of \(2^{\frac{1}{10}}\).
The second expression \(1,\!000 \boldcdot 2^{\frac{h}{10}}\) also helps see that each time \(h\) increases by 10, the exponent increases by 1 and so the expression increases by a factor of 2.
Thinking of the bacterial growth context, for a quantity increasing exponentially, doubling every 10 hours is the same as increasing by a factor of \(2^{\frac{1}{10}}\) each hour.
Lesson Synthesis
Lesson Synthesis
The purpose of this discussion is for students to understand how they can use the properties of exponents to calculate the \(a\) and \(b\) values for an exponential function \(f(x) = a \boldcdot b^x\) starting from two known points on the graph of the function. Display this graph for all to see:

Here are some questions for discussion:
- “Where on a graph do we see the initial value, \(a\), of the function?” (\(a\) is the function value when the input is 0, so \(a\) is where the graph of \(f\) intersects the \(y\)-axis, 300.)
- “What do we know about the function when \(x=1.5\)?” (\(f(1.5)=300 \boldcdot b^{1.5}=153.6\))
- “How can we use \(300 \boldcdot b^{1.5}=153.6\) to calculate the number \(b\)?” (Dividing each side by 300, we have that the decay factor over 1.5 hours is \(\frac{153.6}{300} = 0.512\), which means \(b^{1.5}=0.512\). Using the properties of exponents, \((b^{1.5})^{\frac23}=b\), so \(b=0.64\) because \(0.512^{\frac23}=0.64\).)
- “What equation can we write for this function?” (\(f(x) = 300 \boldcdot (0.64)^x\))
6.4: Cool-down - Finding $a$ and $b$ (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Equations are helpful for communicating how quantities are changing. We can write equations from descriptions or from graphs.
Sometimes, the information on how a quantity is changing is given in a graph instead of in words. We can find an equation for an exponential function using two points on its graph, just as we’ve done in the past with linear functions. Let’s say we want to find a function \(f\) of the form \(f(x) = a \boldcdot b^x\) whose graph contains \((0,64)\) and \((0.5,38.4)\).

Since the point \((0,64)\) is on the graph of \(f\), we know the value of the function at 0 is 64. This means that \(f(0)=a\boldcdot b^0=a\), so the value of \(a\) is 64.
Using the second given point, \((0.5,38.4)\), we know \(f(0.5)=38.4\). This means that \(64 \boldcdot b^{0.5}=38.4\). Solving this equation we have:
\(\begin{align} 64 \boldcdot b^{0.5} &= 38.4 \\ b^{0.5} &= \tfrac{38.4}{64} \\ b^{0.5} &= 0.6\\ \end{align}\)
To determine the exact value of \(b\), let’s use the properties of exponents. Since \(b\) is positive, we can show that \(b=0.36\) because
\(\begin{align} b^{0.5} &=0.6\\ \left(b^{0.5}\right)^2 &= (0.6)^2 \\ b &= 0.36 \end{align}\)
We can now write an equation defining \(f\): \( f(x) = 64 \boldcdot \left(0.36\right)^x\).
