Lesson 14
Putting It All Together
14.1: Equal Slices (5 minutes)
Warm-up
This warm-up invites students to reason about areas of circles and their sectors in the context of cost-efficiency. This context will be explored further in the next activity.
Student Facing
At a pizza restaurant, a personal pizza has a radius of 10 centimeters and costs $5. Another restaurant takes a pizza with radius 30 centimeters, cuts it into 8 slices of equal area, and charges $5 per slice. Which is a better deal? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask for 1 or 2 brief responses from students before moving on to the next activity. The important point is that for the same price, the large slice gives more pizza, making it a better deal.
14.2: Pizza Palooza (25 minutes)
Activity
In this activity, students are building skills that will help them in mathematical modeling (MP4). They formulate a model of a pizza slice as a sector of a circle. They compute unit costs per square inch of pizza to compare the value of several different vendors’ pizza deals. During the activity synthesis, students report their conclusions and the reasoning behind them, and they have an opportunity to consider how to quantify variables beyond price and area.
Making spreadsheet technology available gives students an opportunity to choose appropriate tools strategically (MP5). Monitor for students who use protractors, and for those who use the string to measure arc length and radius. Identify groups who choose their pizza based strictly on cost, and those who also consider other variables such as number of toppings and crust thickness.
Launch
Arrange students in groups of 4. Distribute the following to each group: one set of cards from the blackline master, protractors, string, rulers, and, if possible, digital tools that can run spreadsheet technology. Tell students that they can choose from any of these tools as they work.
Ask students, “When a restaurant advertises a 12-inch pizza, what does that mean?” (The diameter of the pizza measures 12 inches.)
Supports accessibility for: Language; Organization
Student Facing
Elena was researching offers for the upcoming Pizza Palooza festival. She wants to get a good deal on a single slice of pizza.
Your teacher will give you cards that show the deals offered by 4 vendors. Which vendor should Elena choose? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may accidentally use the diameter instead of the radius when calculating circle areas. Ask them what expression they are using to calculate circle areas, and to check if they’ve used correct measurements.
Activity Synthesis
Select previously identified groups to share their choices in this order: First, choose a group who used string to estimate the angle measures in radians. Next, choose a group who used a protractor to estimate the angle measures in degrees. Ask students to compare and contrast the protractor and string strategies. (String is a more common object and so you’re more likely to have it with you. A protractor gives you the angle measure in one step without needing to calculate a ratio. Both give the same answer, just in different units.)
Then, choose a group who chose vendor A because it represents the least expensive unit cost. Then, choose a group who chose a different vendor based on other variables. Ask students how they could quantify some of these other variables. (Students could calculate the volume of the pizza if crust thickness is important to them. They could try to figure out a calorie count if they want the most energy for their money. They could create an expression that assigns relative importance to toppings, size, and crust type.)
Consider asking students, “The photos didn’t show the actual sizes of the pizza slices—the images were scaled down versions of the real thing. Why could we use them to gather information about the areas of the slices?” (Scaling preserves angle measures, so we could use the photos to find the measures of the sectors’ central angles.)
Design Principle(s): Cultivate conversation
14.3: A Fair Split (15 minutes)
Optional activity
In this activity, students have the opportunity to use what they know about trigonometry and circles to decide how to divide a pizza slice between two people equally so that one of them doesn’t have to eat the crust. Students build skills that will help them in mathematical modeling (MP4) as they decide how to represent the situation. Students may define variables, draw diagrams, and use trial and error.
Launch
Arrange students in groups of 2. After quiet work time, ask students to compare their responses to their partner’s and decide if they are both correct, even if they are different. Follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Student Facing
Jada and Andre want to share a big slice of pizza so that each of them gets the same amount, but Andre doesn’t like the crust. The pizza slice is a sector of a circle with a radius of 20 cm and a central angle that measures \(\frac{\pi}{3}\) radians.
How can Andre and Jada divide the slice of pizza into 2 equal pieces so that Andre doesn’t have to eat any crust?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for deciding where to divide the pizza slice. Ask students, “What would change if the radius and central angle were different? What would stay the same?” (The process would be the same. But when the angle increases past a certain point, the isosceles triangle, whose congruent sides are radii, starts to have a smaller area than the rest of the sector, making the problem impossible.)
Design Principle(s): Support sense-making; Optimize output (for justification)
14.4: Let Your Light Shine (15 minutes)
Optional activity
In this activity, students use properties of circumscribed circles and inscribed angles to locate possible positions for a light in a photography session.
Launch
Design Principle(s): Support sense-making
Student Facing
Noah is taking photos of a sculpture he made in art class. He will submit the photos to a contest. The sculpture is in front of a backdrop, which is represented from an overhead view in the image by segment \(AB\). Noah positioned a light at point \(C\) so that the edges of the light beam meet up exactly with the backdrop at segment \(AB\).
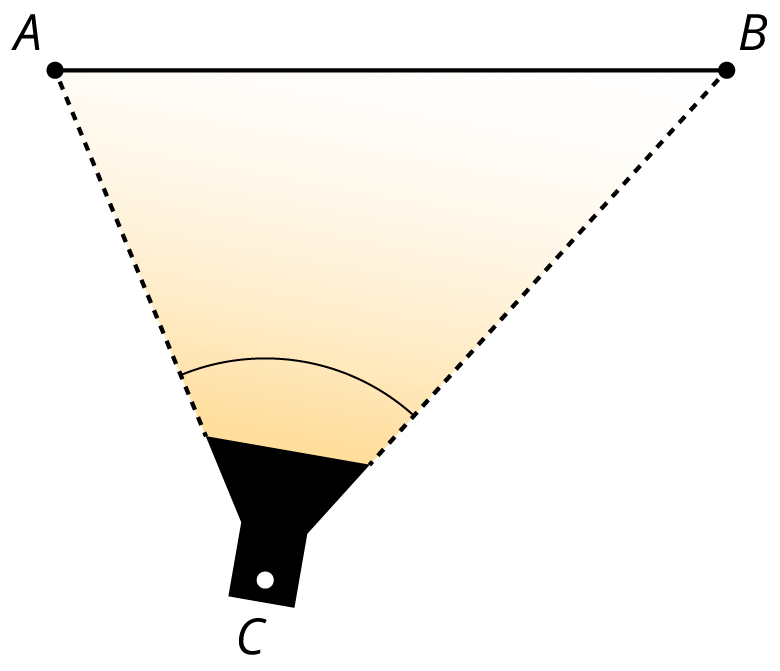
Noah wants to try different positions for the light to highlight different aspects of the sculpture, but he still wants the edges of the beam to exactly meet the endpoints of the backdrop. Find at least 3 other places Noah can place the light. Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students aren’t sure how to begin, remind them of the name of the unit: Circles. Are there any circles that relate to triangles? Are there any other theorems about circles that might help?
Activity Synthesis
Here are some questions for discussion:
- “What are some vocabulary terms from this unit that are relevant to this problem?” (The sides of the beam of light are represented by chords. We needed to find the circumcenter of the triangle to construct the circumscribed circle. The angle made by the sides of the light beam is an inscribed angle.)
- “How many possible positions are there for the light?” (Technically, there are an infinite number of positions. Any point on the circumscribed circle that is in front of the backdrop will work.)
- “What are some other situations where inscribed angles might be relevant?” (A spotlight shining on a stage is similar. Sightlines and viewing angles in auditoriums might involve inscribed angles. There could be applications in design, when creating the spoke pattern of a car wheel or designing a logo for a company.)
Lesson Synthesis
Lesson Synthesis
Ask students to think of other situations where each of these concepts might appear in real life: tangent lines, angles circumscribed about circles, circumcenters, incenters, inscribed circles, arc length, or any other topic from this unit. Consider assigning each group of students one particular topic to think about. Give students 2–3 minutes of time to discuss and brainstorm, then follow with a whole-class discussion.
Sample responses:
- A car wheel touches the ground in 1 point, so the ground is tangent to the car. (The wheel actually flattens and touches the ground in a region, not just 1 point, but we may be able to model this situation with a tangent line.)
- The sightlines of a satellite monitoring the earth can be modeled by a circumscribed angle.
- A circumcenter is a point that is the same distance from 3 vertices, so it can be used when finding fair locations for placements of things like a hospital or a playground.
- An incenter is a point that is the same distance from 3 sides of a triangle, so could be used if we needed to locate, say, a fire station an equal distance from 3 straight roads connecting towns.
- Inscribed circles are the largest circles that can be cut from a triangle, so if we need to cut a circle out of a piece of wood or stone, we might use the inscribed circle.
- Arc length could be used to measure the distance a point on a gear travels during rotation.
Student Lesson Summary
Student Facing
We can use sector areas to compare the value of product offers. Suppose the manager of a store wants to buy several dozen mirrors shaped like sectors of a circle to decorate the store. The manager is choosing between these 2 brands of mirrors at a tradeshow. Brand A’s mirror has radius 14 inches and costs \$35 for each sector. Brand B’s mirror has radius 15 inches and costs \$42. Which is the better deal in terms of cost per square inch of mirror?
brand A

brand B

Brand A’s mirror is made from a circle cut into 6 congruent slices. Using the expression \(\pi r^2\) with radius 14 inches, we find that the area of the full circle is \(196\pi\) or about 616 square inches. Divide that by 6 to find that each sector-shaped mirror has an area of about 103 square inches. At \$35 per sector, this mirror costs about \$0.34 per square inch.
For brand B, we don’t know how many slices the mirror was cut into. However, we can estimate the measure of the central angle using arc length and radius. Suppose the manager uses a flexible measuring tape to find that the length of the arc around the outside of the sector is 19 inches. The ratio of the arc length to the radius gives the measure of the central angle in radians, \(\frac{19}{15}\). This is about 1.27 radians, but to avoid rounding errors, let’s use the exact value, \(\frac{19}{15}\), in our calculations.
Next, we can find the area of the sector with the formula \(\frac12 r^2 \theta\) where \(r\) is the radius and \(\theta\) is the radian measure of the central angle. Substitute in our values to get \(\frac12 (15)^2 \boldcdot \frac{19}{15}\), or 142.5 square centimeters. At \$42 per sector, this mirror costs about \$0.29 per square inch. Brand B’s mirror is a better deal.