Lesson 7
Angle-Side-Angle Triangle Congruence
7.1: Notice and Wonder: Assertion (5 minutes)
Warm-up
The purpose of this warm-up is to highlight some basic assumptions about lines in geometry. Basic assumptions can seem obvious, which makes them difficult to discuss. Students only need to begin thinking about the idea here; they will solidify their understanding when they draw conclusions based on these assumptions during the proof of the Angle-Side-Angle Triangle Congruence Theorem. While students may notice and wonder many things about this statement, logical deductions about the number of intersection points are the important discussion points.
This activity works best when each student has access to the applet because students will benefit from seeing the relationship in a dynamic way. If students don't have individual access, displaying the applet would be helpful as students notice and wonder.
Launch
Display the statement for all to see. Ask students to think of at least one thing they notice and at least one thing they wonder. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Student Facing
What do you notice? What do you wonder?
Assertion: Through two distinct points passes a unique line. Two lines are said to be distinct if there is at least one point that belongs to one but not the other. Otherwise, we say the lines are the same. Lines that have no point in common are said to be parallel.
Therefore, we can conclude: given two distinct lines, either they are parallel, or they have exactly one point in common.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Display the statement for all to see. Ask students to think of at least one thing they notice and at least one thing they wonder. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion.
Display the applet from the digital version of this activity for all to see, or navigate to https://www.geogebra.org/m/kkaqjpnb. For classrooms without internet access, display this image for all to see.
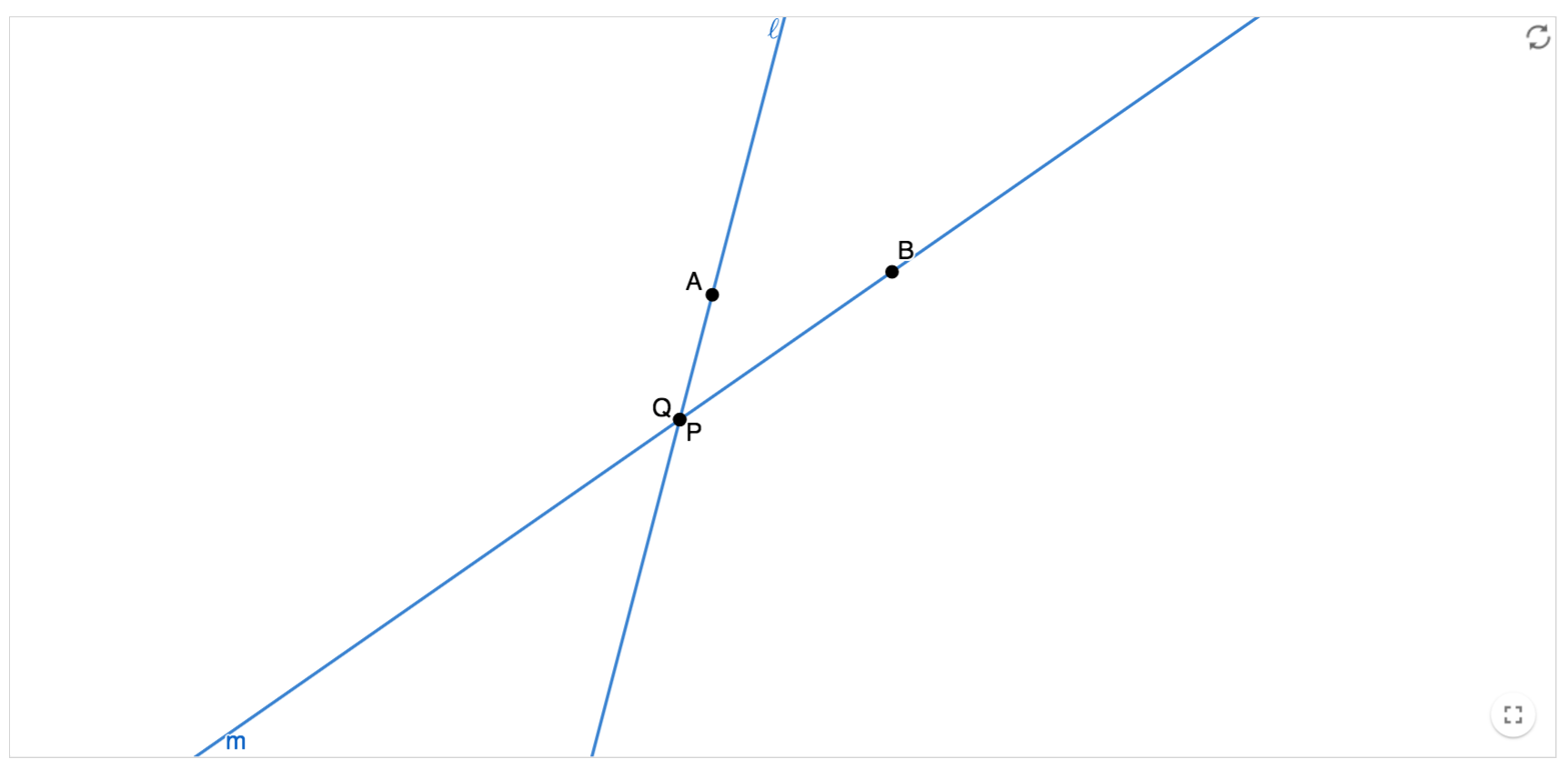
Student Facing
Assertion: Through 2 distinct points passes a unique line. Two lines are said to be distinct if there is at least 1 point that belongs to one but not the other. Otherwise, we say the lines are the same. Lines that have no point in common are said to be parallel.
Therefore, we can conclude: given 2 distinct lines, either they are parallel, or they have exactly 1 point in common.
What do you notice? What do you wonder?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Students will use the fact that two distinct lines can only meet at one point to justify why two points must coincide to write proofs. Focus the discussion on this fact.
Ask students to share the things they noticed and wondered. Record and display their responses for all to see. After all responses have been recorded without commentary or editing, ask students, “Is there anything on this list that you are wondering about now?” Encourage students to respectfully disagree, ask for clarification, or point out contradicting information. If the fact that if two distinct lines intersect then the points must coincide does not come up during the conversation, here are some questions for discussion:
- In the applet line \(\ell\) passes through point \(A\) and point \(P\). Line \(m\) passes through point \(B\) and point \(Q\). In the starting position line \(\ell\) also passes through point \(Q\) and line \(m\) also passes through point \(P\).
- If line \(\ell\) and line \(m\) are distinct, what must be true about points \(P\) and \(Q\)? (They must coincide or be the same point.)
- If points \(A\) and \(B\) are distinct, what must be true about lines \(\ell\) and \(m\)? (They must be distinct, and not parallel.)
Use the applet to demonstrate each condition.
7.2: Proving the Angle-Side-Angle Triangle Congruence Theorem (15 minutes)
Activity
In this activity, students consider how to adapt the Side-Angle-Side Triangle Congruence proof they wrote in a previous lesson to the case in which the given information is two pairs of congruent corresponding angles and a pair of congruent corresponding sides between the angles. There is less structure provided in this activity than in previous proofs, so monitor for students who need support.
Identify students who provide varying levels of precision in their explanation that the final pair of vertices coincide.
Making dynamic geometry software available gives students an opportunity to choose appropriate tools strategically (MP5).
Launch
Arrange students in groups of 2. After a minute of quiet work time, ask students to compare sketches with a partner and tell their partner how they know their sketch matches the given information. (This should ensure the included side is the one marked as congruent. It is not necessary to use the term included with students.)
Remind students to refer to their examples of proofs and the display of sentence frames.
If students have access to GeoGebra Geometry from Math Tools, suggest that it might be a helpful tool in this activity.
Design Principle(s): Cultivate conversation
Supports accessibility for: Language; Social-emotional skills
Student Facing
- Two triangles have 2 pairs of corresponding angles congruent, and the corresponding sides between those angles are congruent. Sketch 2 triangles that fit this description.
- Label the triangles \(WXY\) and \(DEF\), so that angle \(W\) is congruent to angle \(D\), angle \(X\) is congruent to angle \(E\), and side \(WX\) is congruent to side \(DE\).
- Use a sequence of rigid motions to take triangle \(WXY\) onto triangle \(DEF\). For each step, explain how you know that one or more vertices will line up.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
“Think about how the information you have now is different from the information you had earlier. Work with your partner to change the proofs you used earlier to match the Angle-Side-Angle information given.”
Activity Synthesis
Display this image for all to see and ask, “Could the situation look like this after we reflect across \(DE\)? How do you know?”

Invite multiple students to share their reasoning for why vertices \(Y\) and \(F\) had to coincide. Questions to help students make their reasoning more precise include:
- If students assumed that \(Y\) is the same distance along the ray as \(F\) is: We don’t know how far \(Y\) is from \(W\) and \(X\), or how far \(F\) is from \(D\) and \(E\). Is there another way you could prove they were in the same place?
- If students assert that two rays can only intersect in one place but don’t say anything about how we know the points are on the same rays: How do you know that the rays that point \(Y\) is on are the same as the rays that point \(F\) are on?
- If students say, “because they are on the same rays” but don’t mention the intersection: Why can’t those rays intersect in more than one place?
After multiple students have shared and clarified their reasoning, point out that this is a new reason why vertices have to coincide. Add this to the display of sentence frames for proofs. This display should be posted in the classroom for the remaining lessons within this unit. You will add to the display throughout the unit. An example template is provided in the blackline masters for this lesson.
Justifications:
- Points \(\underline{\hspace{1in}}\) and \(\underline{\hspace{1in}}\) coincide because they are both at the intersection of the same lines, and two distinct lines can only intersect in one place.
Ask students to add the Angle-Side-Angle Triangle Congruence Theorem to their reference charts as you ceremoniously add it to the class reference chart:
Angle-Side-Angle Triangle Congruence Theorem: In two triangles, if two pairs of corresponding angles, and the pair of corresponding sides between the angles, are congruent, then the triangles must be congruent. (Theorem)
\(\angle A \cong \angle C, \overline{AE} \cong \overline{EC}, \angle DEA \cong \angle BEC\), so \(\triangle DEA \cong \triangle BEC\)

7.3: Find the Missing Angle Measures (5 minutes)
Optional activity
If students struggled with the question on parallel lines and a transversal on the previous end of unit test, use this optional activity to remind students that alternate interior angles formed by parallel lines and a transversal are congruent in preparation for subsequent activities.
Launch
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Lines \(\ell\) and \(m\) are parallel. \(a = 42\). Find \(b\), \(c\), \(d\), \(e\), \(f\), \(g\), and \(h\).
\(\ell \parallel m\)

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students about their reasoning for the relationship between different pairs of angles in this order:
- \(a\) and \(b\) (the angles form a linear pair)
- \(a\) and \(c\) (the angles are vertical angles)
- \(a\) and \(e\) (the angles are corresponding angles)
- \(c\) and \(e\) (the angles are alternate interior angles)
If students describe how they found \(c\) and \(e\) by referring back to them both being equal to \(a\), first congratulate them on an accurate use of the transitive property, then ask students if they recall the name of the angle pair that the angles with measures \(c\) and \(e\) form, and if needed, remind them of the term alternate interior angles. Having a single statement about the angles with measure \(c\) and \(e\) makes later proofs that rely on their relationship much simpler to describe.
7.4: What Do We Know For Sure About Parallelograms? (15 minutes)
Activity
The goal of this activity is for students to see the usefulness of the triangle congruence theorems in proving other results. In this proof, students are expected to draw an auxiliary line that allows them to use the Angle-Side-Angle Triangle Congruence Theorem. Through articulating things they notice and things they wonder about in the diagrams, students have an opportunity to attend to precision in the language they use to describe what they see (MP6).
Students may also choose to prove the triangles are congruent because they are \(180^{\circ}\) rotations of one another, which is fine. If students use any technique other than the Angle-Side-Angle Triangle Congruence Theorem, discuss that the Angle-Side-Angle Triangle Congruence Theorem is a shortcut to use without having to write out the transformations and reasons each time.
Making dynamic geometry software available gives students an opportunity to choose appropriate tools strategically (MP5)
Launch
Give students 3 minutes of work time, then pause the activity. Select two students’ drawings with the auxiliary line to display for all to see—one with each diagonal. Use the Notice and Wonder instructional routine to elicit what students notice in their peers' diagrams.
Ask students to think of at least one thing they notice and at least one thing they wonder. Give students 1 minute of quiet think time, and then 1 minute to discuss the things they notice with their partner, followed by a whole-class discussion. Focus the discussion on what might be congruent.
Things students may notice:
- There are two different diagonals drawn
- Each diagram now has two triangles
- The diagrams are not the same
Things students may wonder:
- Are the triangles congruent?
- Are the sides of the parallelogram congruent?
Draw students’ attention to the definition of a parallelogram, and point out that we are probably going to use that in the proof. Ask students to add this definition to their reference charts as you add it to the class reference chart:
A parallelogram is a quadrilateral with two pairs of opposite sides parallel. (Definition)
\(\overline{NM} \parallel \overline{KL}, \overline{NK} \parallel \overline{NL}\), so \(MNKL\) is a parallelogram

Supports accessibility for: Visual-spatial processing;Conceptual processing; Organization
Student Facing
Quadrilateral \(ABCD\) is a parallelogram. By definition, that means that segment \(AB\) is parallel to segment \(CD\), and segment \(BC\) is parallel to segment \(AD\).
- Sketch parallelogram \(ABCD\) and then draw an auxiliary line to show how \(ABCD\) can be decomposed into 2 triangles.
- Prove that the 2 triangles you created are congruent, and explain why that shows one pair of opposite sides of a parallelogram must be congruent.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
When we have 3 consecutive vertices of a polygon \(A\), \(B\), and \(C\) so that the triangle \(ABC\) lies entirely inside the polygon, we call \(B\) an ear of the polygon.
- How many ears does a parallelogram have?
- Draw a quadrilateral that has fewer ears than a parallelogram.
- In 1975, Gary Meisters proved that every polygon has at least 2 ears. Draw a hexagon with only 2 ears.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle longer than is productive, direct them to their reference charts. What do they know about parallel lines? (Alternate interior angles are congruent.)
Activity Synthesis
If any students used a transformation-based proof, invite them to share their thinking, and then compare their work to students who used the Angle-Side-Angle Triangle Congruence Theorem. Compare the reasoning in the transformation proof to the reasoning used in the proof of the Angle-Side-Angle Triangle Congruence Theorem that happened earlier in the lesson. Inform students the Angle-Side-Angle Triangle Congruence Theorem is a shortcut for a whole chain of reasoning about why vertices must coincide.
If no students used a transformation proof, there is no need to introduce one. Focus the discussion on what were the easy parts of writing the proof and what were the hard parts. Work toward identifying these components of using triangle congruence criteria in proofs:
- You need to find triangles that are congruent.
- You might need to draw an auxiliary line.
- You need to find three parts of the triangles that are congruent (Side-Angle-Side or Angle-Side-Angle).
- You might need to use something like alternate interior angles—it’s not always given to you why the angles or sides are congruent.
- Once you find the right three parts, then you know the triangles are congruent, so then any of their pairs of corresponding parts are congruent.
Ask students to add this theorem to their reference charts as you add it to the class reference chart:
In a parallelogram, pairs of opposite sides are congruent. (Theorem)
\(MNKL\) is a parallelogram so \(\overline{NM} \cong \overline{KL}, \overline{NK} \cong \overline{ML}\)

Design Principle(s): Support sense-making; Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
Remind students of the (at least) two different proofs they’ve done that involved the Angle-Side-Angle or Side-Angle-Side Triangle Congruence Theorems.
Arrange students in groups of 2. Instruct students to work with their partner to brainstorm a list of hints or steps that will help other students write proofs that use triangle congruence theorems.
Monitor for partners discussing:
- adding auxiliary lines
- looking for congruent triangles
- needing (the right) three pieces of information about the triangle
- using the marks on the diagrams and the given information
- using other information like angles formed by parallel lines
- using congruent triangles to prove that other pairs of corresponding segments or angles are congruent
Call on students in an order that roughly matches the order above, so that their advice goes in the steps of the proof process. Create a display of tips for proving lines, angles, or triangles are congruent using triangle congruence theorems. This display should be posted in the classroom for the remaining lessons within this unit. An example is provided in the blackline masters for this lesson.
7.5: Cool-down - Both (Pairs of) Sides Now (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We know that in 2 triangles, if 2 pairs of corresponding sides and the pair of corresponding angles between the sides are congruent, then the triangles must be congruent. But we don’t always know that 2 pairs of corresponding sides are congruent. For example, when proving that opposite sides are congruent in any parallelogram, we only have information about 1 pair of corresponding sides. That is why we need other ways than the Side-Angle-Side Triangle Congruence Theorem to prove triangles are congruent.
In 2 triangles, if 2 pairs of corresponding angles and the pair of corresponding sides between the angles are congruent, then the triangles must be congruent. This is called the Angle-Side-Angle Triangle Congruence Theorem.

When proving that 2 triangles are congruent, look at the diagram and given information and think about whether it will be easier to find 2 pairs of corresponding angles that are congruent or 2 pairs of corresponding sides that are congruent. Then check if there is enough information to use the Angle-Side-Angle Triangle Congruence Theorem or the Side-Angle-Side Triangle Congruence Theorem.
The Angle-Side-Angle Triangle Congruence Theorem can be used to prove that, in a parallelogram, opposite sides are congruent. A parallelogram is defined to be a quadrilateral with 2 pairs of opposite sides parallel.

We could prove that triangles \(ABC\) and \(CDA\) are congruent by the Angle-Side-Angle Triangle Congruence Theorem. Then we can say segment \(AD\) is congruent to segment \(CB\) because they are corresponding parts of congruent triangles.