Lesson 2
When and Why Do We Write Quadratic Equations?
2.1: How Many Tickets? (5 minutes)
Warm-up
This warm-up activates what students know about interpreting equations in context and about solving for a variable. The given equation is linear and is relatively straightforward. The work prepares students to reason about quadratic equations in the lesson.
To find the unknown input in each question, students might:
- Try different values of \(t\) until they find one that yields the specified value of \(c\).
- Reason backwards (subtract 2.5 from 62.50 and then divide the result by 12) without writing out the steps.
- Solve \(62.5=12t+2.5\) and \(278.5=12t+2.5\) by performing the same operation to each side to isolate \(t\).
Student Facing
The expression \(12t + 2.50\) represents the cost to purchase tickets for a play, where \(t\) is the number of tickets. Be prepared to explain your response to each question.
- A family paid $62.50 for tickets. How many tickets were bought?
- A teacher paid $278.50 for tickets for her students. How many tickets were bought?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their responses and reasoning. Highlight the different strategies used to answer the questions.
If no students thought of the situation in terms of a function and wrote an equation, point out that we can think about cost as being a function of the number of tickets. In answering the questions, we were looking for the inputs that produce different outputs. This can be done by solving equations. In the case of linear equations, we can “do the same thing to each side” to isolate the variable.
2.2: The Flying Potato Again (15 minutes)
Activity
This task prompts students to try different ways to solve a quadratic equation. They are familiar with solving equations by performing the same operation to each side of an equation, but here they see that this is not really a workable strategy. Students are also discouraged from using a graph to solve the equation. Because they do not yet know an efficient way to use algebra to solve \( \text-16t^2 + 80t + 64=0\), they need to try different strategies and persevere in problem solving (MP1).
As students work, notice those who use strategies listed in the Activity Synthesis. Ask them to share their approach during discussion.
Launch
Arrange students in groups of 2. Give them a few minutes of quiet think time and then time to collaborate on solving the equations.
No graphing technology should be used in this activity.
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
The other day, you saw an equation that defines the height of a potato as a function of time after it was launched from a mechanical device. Here is a different function modeling the height of a potato, in feet, \(t\) seconds after being fired from a different device:
\(\displaystyle f(t) = \text-16t^2 + 80t + 64\)
- What equation would we solve to find the time at which the potato hits the ground?
- Use any method except graphing to find a solution to this equation.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Poll the class on their solutions to the equation and record and display the solutions for all to see. Then, ask some students to share their strategies and any associated challenges. If not mentioned by students, discuss the limitations of these approaches:
- Isolating the variable: If we try to solve by performing the same operation to each side of the equation, we quickly get stuck.
\(\displaystyle \begin {align} \text-16t^2 + 80t + 64 &=0 &\qquad& \text {Original equation}\\\\ \text-16t^2 + 80t &= \text-64 &\qquad& \text {Subtract 64 from each side}\\\\ t^2-5t &=4 &\qquad& \text {Divide each side by -16}\\ \end {align}\)
But then what? If we add \(5t\) to each side, we now have a variable on both sides and cannot combine any like terms. We could multiply or divide each side by any constant we wish, but we are no closer to isolating \(t\).
-
Guessing and checking: We can evaluate the quadratic expression at different values of \(t\) until the expression has a value that is 0 or close to 0. For example, when \(t\) is 4, the expression has a value of 128. At \(t=5\), it has a value of 64, and at \(t=6\), it has a value of -32. That means \(t\) is between 5 and 6, so we need to try different decimal values in that range.
This process is laborious, and may not get us to a precise solution.
-
Graphing: Students may suggest that a graph would allow them to solve the problem much more quickly. Use graphing technology to demonstrate that if we graph the equation \(y=f(t)\), an approximate solution given is 5.702, as shown in the image.
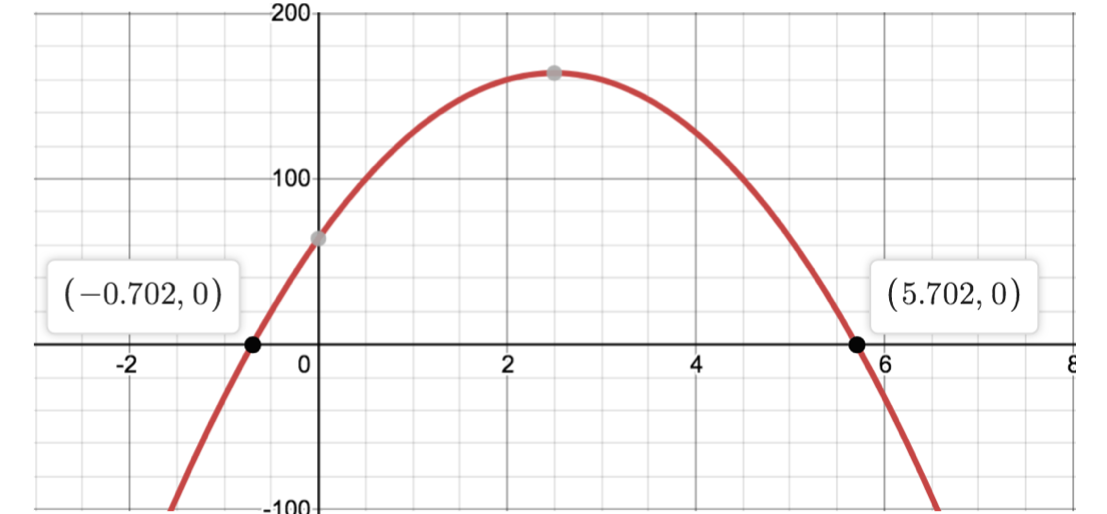
If we evaluate \(f(5.702)\), however, we get roughly -0.044864, rather than exactly 0.
A graph is useful for approximating values, but it isn’t always possible to use it to find exact values.
Tell students that in this unit they will learn some efficient strategies for solving equations like these.
Supports accessibility for: Visual-spatial processing; Conceptual processing
2.3: Revenue from Ticket Sales (15 minutes)
Activity
This activity aims to show that it is relatively easy to solve a quadratic equation when one side of the equation is zero and the other side is a quadratic expression in factored form, and that it may be a little tricky to solve the equation otherwise.
The activity prompts students to recall what they learned in an earlier unit, that the zeros of a function correspond to the horizontal intercepts of the graph representing that function, and that the zeros are the solutions to an equation of the form \(\text{quadratic expression} = 0\).
As students make sense of the equations and ways to use them to solve a contextual problem, they practice reasoning quantitatively and abstractly (MP2).
Launch
Keep students in groups of 2.
Read the opening paragraph in the task statement. Give students a moment to think about how much the school would collect if they sell the tickets at $5 each (it would collect $875). Briefly survey how they found out the answer. (Students are likely to have used the factored form because it lends itself to simpler calculations.)
Ask students to recall the form in which each quadratic expression is written. Then, give them a minute to talk to a partner and recall at least two things about each form and what the form might tell us about the graph of the function that the expression defines.
Record their responses for all to see. If no students mentioned the connection between either of the forms to the horizontal intercepts of the graph or the zeros of the function, ask them about it.
Tell students that they do not need to find the ticket prices in the second question, but only to think about how to go about doing so.
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
The expressions \(p(200-5p)\) and \(\text-5p^2 + 200p\) define the same function. The function models the revenue a school would earn from selling raffle tickets at \(p\) dollars each.
- At what price or prices would the school collect $0 revenue from raffle sales? Explain or show your reasoning.
- The school staff noticed that there are two ticket prices that would both result in a revenue of $500. How would you find out what those two prices are?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Can you find the following prices without graphing?
- If the school charges $10, it will collect $1,500 in revenue. Find another price that would generate $1,500 in revenue.
-
If the school charges $28, it will collect $1,680 in revenue. Find another price that would generate $1,680 in revenue.
- Find the price that would produce the maximum possible revenue. Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students struggle to connect the expressions that define the function to the questions, ask them what the input and output of the function represent. If students struggle with the first question, ask them what values of \(p\) would yield a value of 0 for the expression.
Activity Synthesis
Invite students to share their responses and strategies. Make sure students see that the first question can be represented by solving the equation \(p(200-5p)=0\), and that the second question can be represented by solving either \(p(200-5p)=500\) or \(\text-5p^2 + 200p=500\).
Although students are not yet formally introduced to the zero product property, they do have experience with finding the zeros of a quadratic function when given an expression in factored form. This prior knowledge enables them to reason about the solutions to the equation \(p(200-5p)=0\). For instance, noticing the factor \(p\), students are likely to say that one zero of the function is 0.
Ask students,
- “How can you show, without graphing, that \(p=0\) will produce no revenue, or that it is a solution to the equation \(p(200-5p)=0\)?” (When \(p =0\), the factor \(p\) is 0 and therefore the entire expression equals 0.)
- “How can you show that \(p=40\) will also produce no revenue, or that it is also a solution to the same equation?” (When \(p=40\), the factor \((200-5p)\) is 0, and likewise, the entire expression is 0.)
- “Can we use the same reasoning to find the solutions to \(p(200-5p)=500\) or \(\text-5p^2 + 200p =500\)? Why or why not?” (No, not easily. Neither show the zeros of a function. There are many pairs of factors that have 500 as a product.)
Make sure students see that it is fairly straightforward to find the solutions to equations such as \(p(200-5p)=0\), but the same cannot be said about equations such as \(p(200-5p)=500\) or \(\text-5p^2 + 200p =500\).
Highlight that all the equations in this activity are quadratic equations. Explain that a quadratic equation is one that can be written in the form of \(ax^2+bx+c=0\), and where \(a\) is not 0.
If time permits, ask students to show how all of the equations seen here can be written in this form.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Lesson Synthesis
Lesson Synthesis
Help students to reflect on the key ideas of the lesson by discussing, as a class or with a partner, questions such as:
- “What are some limitations of solving \(\text-2x^2 -2x +40=10\) by guessing and checking? What about by graphing?”
- “Which equation do you think is easier to solve: \(\text-2x^2 -2x +40=0\) or \((8-2x)(x+5)=0\)? Why?”
- “Which is easier to solve: \((8-2x)(x+5)=10\) or \(\text-2x^2 -2x +40=10\)? Why?”
2.4: Cool-down - The Movie Theatre (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The height of a potato that is launched from a mechanical device can be modeled by a function, \(g\) with \(x\) representing time in seconds. Here are two expressions that are equivalent and both define function \(g\).
\(\text-16x^2+80x+96\)
\(\text-16(x-6)(x+1)\)
Notice that one expression is in standard form and the other is in factored form.
Suppose we wish to know, without graphing the function, the time when the potato will hit the ground. We know that the value of the function at that time is 0, so we can write:
\(\text-16x^2+80x+96=0\)
\(\text-16(x-6)(x+1)=0\)
Let's try solving \(\text-16x^2+80x+96 = 0\), using some familiar moves. For example:
- Subtract 96 from each side:
\(\text-16x^2+80x=\text-96\)
- Apply the distributive property to rewrite the expression on the left:
\(\text-16(x^2-5x)=\text-96\)
- Divide both sides by -16:
\(x^2-5x=6\)
- Apply the distributive property to rewrite the expression on the left:
\(x(x-5)=6\)
These steps don’t seem to get us any closer to a solution. We need some new moves!
What if we use the other equation? Can we find the solutions to \(\text-16(x-6)(x+1)=0\)?
Earlier, we learned that the zeros of a quadratic function can be identified when the expression defining the function is in factored form. The solutions to \(\text-16(x-6)(x+1)=0\) are the zeros to function \(g\), so this form may be more helpful! We can reason that:
- If \(x\) is 6, then the value of \(x-6\) is 0, so the entire expression has a value of 0.
- If \(x\) is -1, then the value of \(x+1\) is 0, so the entire expression also has a value of 0.
This tells us that 6 and -1 are solutions to the equation, and that the potato hits the ground after 6 seconds. (A negative value of time is not meaningful, so we can disregard the -1.)
Both equations we see here are quadratic equations. In general, a quadratic equation is an equation that can be expressed as \(ax^2+bx+c=0\) where \(a\), \(b\), and \(c\) are constants and \(a \neq 0\).
In upcoming lessons, we will learn how to rewrite quadratic equations into forms that make the solutions easy to see.