Lesson 17
Volume and Density
- Let’s use volume and density to solve problems.
Problem 1
The washer in the image has an inner diameter of \(\frac14\) inch. The outer diameter measures \(\frac34\) inch, and the washer is \(\frac14\) inch thick. The density of the metal the washers are made of is 0.285 pounds per cubic inch.
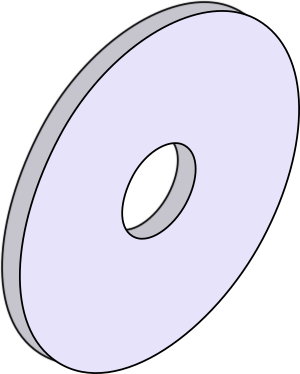
How much do 5 washers weigh, in pounds? Round your answer to the nearest hundredth.
Problem 2
Assume that a cell is a sphere with radius \(10^{\text-3}\) or 0.001 centimeter, and that a cell’s density is 1.1 grams per cubic centimeter.
- Koalas weigh 6 kilograms on average. How many cells are in the average koala?
- Hippos weigh 1,400 kilograms on average. How many cells are in the average hippo?
Problem 3
The density of water is 1 gram per cm3. An object floats in water if its density is less than water’s density, and it sinks if its density is greater than water’s. Will a toy in the shape of a rectangular prism that is 1 centimeter by 2 centimeter by 2 centimeter with mass 3 grams sink or float? Explain your reasoning.
Problem 4
A cube and a sphere both have volume 512 cubic units. Which solid has a greater surface area? Explain your reasoning.
Problem 5
Give the dimensions of 2 solids with equal surface area and different volume.
Problem 6
A right cone has a base with diameter 10 units. The volume of the cone is \(100\pi\) cubic units. What is the length of a segment drawn from the apex to the edge of the circular base?
5 units
12 units
13 units
15 units
Problem 7
A pyramid has a height of 4 inches and a volume of 40 cubic inches. Select all figures that could be the base for this pyramid.
a 5 inch by 2 inch rectangle
a 3 inch by 10 inch rectangle
a triangle with height 10 inches and base 3 inches
a right triangle with one side 5 inches and the hypotenuse 13 inches
a heart with area 30 square inches
Problem 8
Select all solids for which the formula \(V=Bh\) applies.
a triangular prism
a triangular pyramid
a square pyramid
a rectangular prism
a cone
a cylinder
Problem 9
Two distinct lines, \(\ell\) and \(m\), are each perpendicular to the same line \(n\). A fourth distinct line, \(k\), is also perpendicular to line \(n\). Does line \(k\) intersect line \(\ell\) or line \(m\)? Explain how you know.