Lesson 8
Exponential Situations as Functions
Let’s explore exponential functions.
8.1: Rainfall in Las Vegas
Here is a graph of the accumulated rainfall in Las Vegas, Nevada, in the first 60 days of 2017.
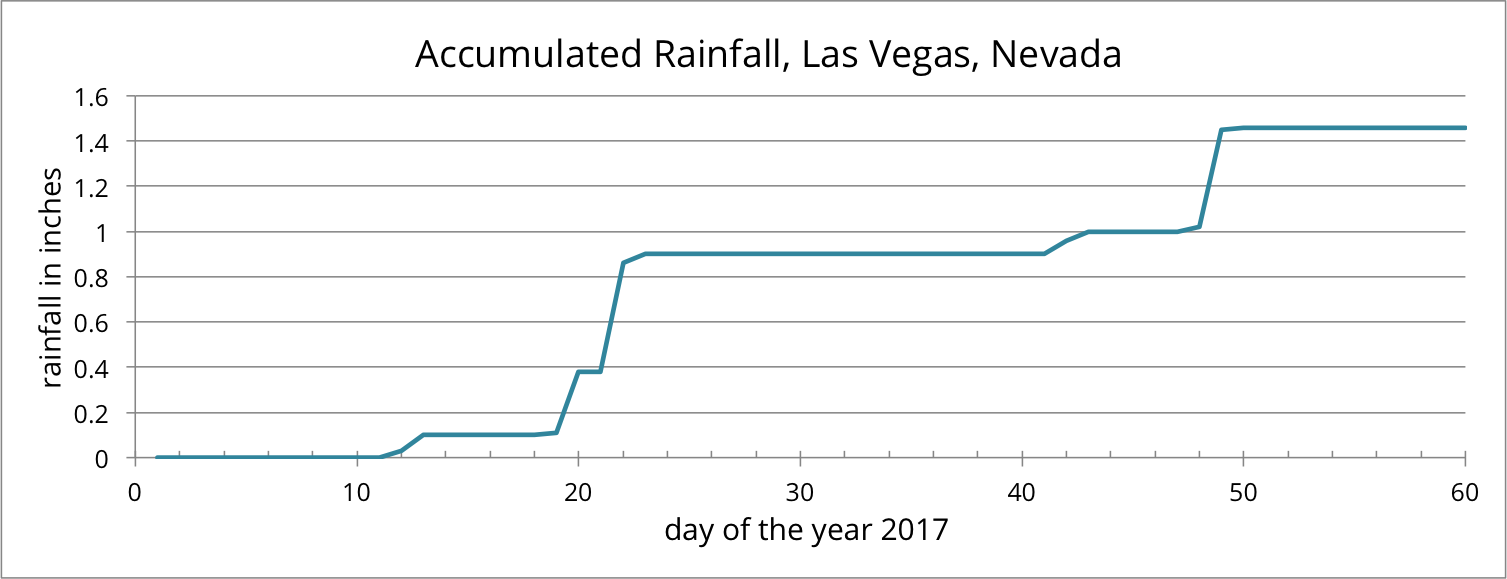
Use the graph to support your answers to the following questions.
- Is the accumulated amount of rainfall a function of time?
- Is time a function of accumulated rainfall?
8.2: Moldy Bread
Clare noticed mold on the last slice of bread in a plastic bag. The area covered by the mold was about 1 square millimeter. She left the bread alone to see how the mold would grow. The next day, the area covered by the mold had doubled, and it doubled again the day after that.
- If the doubling pattern continues, how many square millimeters will the mold cover 4 days after she noticed the mold? Show your reasoning.
- Represent the relationship between the area \(A\), in square millimeters, covered by the mold and the number of days \(d\) since the mold was spotted using:
- A table of values, showing the values from the day the mold was spotted through 5 days later.
- An equation
- A graph
- Discuss with your partner: Is the relationship between the area covered by mold and the number of days a function? If so, write ____ is a function of ____. If not, explain why it is not.
What do you think an appropriate domain for the mold area function \(A\) is? Explain your reasoning.
8.3: Functionally Speaking
Here are some situations we have seen previously. For each situation:
- Write a sentence of the form "\(\underline{\hspace{0.5in}}\) is a function of \(\underline{\hspace{0.5in}}\)."
- Indicate which is the independent and which is the dependent variable.
- Write an equation that represents the situation using function notation.
- In a biology lab, a population of 50 bacteria reproduce by splitting. Every hour, on the hour, each bacterium splits into two bacteria.
- Every year after a new car is purchased, it loses \(\frac13\) of its value. Let’s say that the new car costs $18,000.
- In order to control an algae bloom in a lake, scientists introduce some treatment products. The day they begin treatment, the area covered by algae is 240 square yards. Each day since the treatment began, a third of the previous day’s area (in square yards) remains covered by algae. Time \(t\) is measured in days.
8.4: Deciding on Graphing Window
The equation \(m = 20\boldcdot (0.8)^h\) models the amount of medicine \(m\) (in milligrams) in a patient’s body as a function of hours, \(h\), after injection.
- Without using a graphing tool, decide if the following horizontal and vertical boundaries are suitable for graphing this function. Explain your reasoning.
\(\displaystyle \text-10< h<100\)
\(\displaystyle \text-100< m<1,000\) - Verify your answer by graphing the equation using graphing technology, and using the given graphing window. What do you see? Sketch or describe the graph.
- If your graph in the previous question is unhelpful, modify the window settings so that the graph is more useful. Record the window settings here. Convince a partner why the horizontal and vertical boundaries that you set are better.
Summary
The situations we have looked at that are characterized by exponential change can be seen as functions. In each situation, there is a quantity—an independent variable—that determines another quantity—a dependent variable. They are functions because any value of the independent variable corresponds to one and only one value of the dependent variable. Functions that describe exponential change are called exponential functions.
For example, suppose \(t\) represents time in hours and \(p\) is a bacteria population \(t\) hours after the bacteria population was measured. For each time \(t\), there is only one value for the corresponding number of bacteria, so we can say that \(p\) is a function of \(t\) and we can write this as \(p = f(t)\).
If there were 100,000 bacteria at the time it was initially measured and the population decreases so that \(\frac{1}{5}\) of it remains after each passing hour, we can use function notation to model the bacteria population:
\(\displaystyle f(t) = 100,\!000 \boldcdot \left(\frac{1}{5}\right)^t\)
Notice the expression in the form of \(a \boldcdot b^t\) (on the right side of the equation) is the same as in previous equations we wrote to represent situations characterized by exponential change.
Glossary Entries
- exponential function
An exponential function is a function that has a constant growth factor. Another way to say this is that it grows by equal factors over equal intervals. For example, \(f(x)=2 \boldcdot 3^x\) defines an exponential function. Any time \(x\) increases by 1, \(f(x)\) increases by a factor of 3.